矩阵分解视角下的线性代数
本文是对线性代数核心知识的回顾梳理,主要参考 GILBERT STRANG 的 Linear Algebra and Learning from Data 书本里的 Part I, 更多是从多个不同的矩阵分解视角来看待问题。核心包括:
- 利用 CR 分解证明矩阵行空间秩等于列空间秩 – 用算法进行数学证明
- 利用 LU 分解以及求解方程组 Ax=0 的手段证明 rank-nullity 定理 – 线性方程组意义的引入
- 通过计算方阵的特征值和特征根对矩阵进行对角化分解 – 线性变换、换基变换等几何意义的引入
- 向量和矩阵范数 – "距离"概念和优化问题的引入
- SVD 分解 – 统筹以上所有性质,展现数学本身的美感
- 利用协方差的对角化分解或者 SVD 分解进行 PCA – 统计意义的引入
CR 分解和矩阵乘法
Ax=b、 列空间和分块乘法
Ax=b 更多来自于对方程组的符号抽象,比如线性方程组两个等式:
\[ \left\{\begin{aligned} ax_1 + bx_{2} &= b_1 \\ cx_1 + dx_{2} &= b_2 \end{aligned} \right. \]
就可以抽象成:
\[ \begin{bmatrix} a & b \\c& d \end{bmatrix} \begin{bmatrix} x_{1} \\ x_{2} \end{bmatrix} = \begin{bmatrix} b_1 \\ b_2 \end{bmatrix}\]
这里实际定义了矩阵和向量的乘法,相比于初等代数或微积分里只处理普通的数或函数,Ax=b 中引入了新的数据结构(矩阵、向量)和算法(它们之间的乘法规则)。
这直接体现在 python 中,原始的 python 里可以支持数的相乘:
a=2; x=3
a*x
6
但不支持嵌套数组和数组进行相乘:
A=[[1,2],[3,4]]; x=[1,0]
A*x
TypeErrorTraceback (most recent call last)
<ipython-input-30-236880e16134> in <module>
1 A=[[1,2],[3,4]]; x=[1,0]
----> 2 A*x
TypeError: can't multiply sequence by non-int of type 'list'
因此 numpy 引入了 ndarray 数据结构来统一表示矩阵和向量,并且添加了新的乘法: np.dot 或用新的运算符 @ 表示:
import numpy as np
A=np.array([[1,2],[3,4]]); x=np.array([[1],[0]])
print(np.dot(A, x))
print(A@x)
[[1] [3]] [[1] [3]]
对于矩阵,可以看作是多个独立的数字排列在矩形格子中,也可以看作是多个列向量左右并列的结果,这是一种聚类的视角,就像我们数数的时候可以按照 1,2,3 一个一个地数,也可以 2,4,6 逢双地去数。如果把列向量作为矩阵数据结构的基本组成的话,那么 Ax=b 表示 b 是矩阵 A 中列的加权组合– 也叫线性组合,组合的权重就是 x 向量里的各个值,比如以下 a1 和 a2 是列向量:
\[ \begin{bmatrix} \mathbf{a_{1}} & \mathbf{a_{2}} \end{bmatrix} \begin{bmatrix} x_{1} \\ x_{2} \end{bmatrix} = x_1 \mathbf{a_{1}} + x_2 \mathbf{a_{2}}\]
把矩阵 A 的列向量的线性组合的所有可能向量集合称为 A 的列空间,可以记为 Col(A) 或 C(A) 。
在更深入理解 C(A) 有哪些特殊性质之前,先取一些极端的 x 向量的例子来展示这个空间里有什么,并理解一些典型向量在矩阵乘以向量中起到的作用。例如:
\[ \begin{bmatrix} \mathbf{a_{1}} & \mathbf{a_{2}} \end{bmatrix} \begin{bmatrix} 1 \\ 0 \end{bmatrix} = \mathbf{a_{1}}\]
以上 x 是一个标准单位向量, Ax 的结果是 A 矩阵的第一列,同样,如果取 \( x=\begin{bmatrix} 0 \\ 1 \end{bmatrix} \),那么得到的是 A 的第二列 a2 。因此,标准单位向量可以看作是列选择器,假设 \( e_{i} \) 表示 1 在第 i 个位置的单位向量,那么 \( Ae_{i} \) 就是 A 的第 i 列 \( a_{i} \) 。 这种向量在深度学习里叫作 one-hot, 它核心作用就是用来选择,就像 numpy 中对 ndarray 切片选择机制一样(只是下标从 0 开始),以下两个结果是一样的,实际中更偏向于用切片去选择,因为这是"底层"实现,效率更高,但如果需要维持数学上的性质(比如证明某些数学定理),则可以用矩阵乘法来表示,这样可以通过"高层"乘法的通用性质做推理。
print(A[:,0:1])
print(A@x)
[[1] [3]] [[1] [3]]
其他的一些带有具体操作意义的向量:
- 差分: \( \begin{bmatrix} \mathbf{a_{1}} & \mathbf{a_{2}} \end{bmatrix} \begin{bmatrix} 1 \\ -1 \end{bmatrix} = \mathbf{a_{1}} - \mathbf{a_{2}} \)
- 平均(池化): \( \begin{bmatrix} \mathbf{a_{1}} & \mathbf{a_{2}} \end{bmatrix} \begin{bmatrix} \frac{1}{2} \\ \frac{1}{2} \end{bmatrix} = (\mathbf{a_{1}}+\mathbf{a_{2}})/2\)
另一方面,将 A 看作列的组合是一种偏"机械"的操作,像是在黑板上用尺子来划定区域,这种操作可以继续扩展,比如对 A 每一列添加一个 0:
\[ \begin{bmatrix} a & b \\c& d \\ 0 & 0 \end{bmatrix} \begin{bmatrix} x_{1} \\ x_{2} \end{bmatrix} = \begin{bmatrix} b_1 \\ b_2 \\ 0 \end{bmatrix}\]
写成列形式:
\[ \begin{bmatrix} \mathbf{a_{1}} & \mathbf{a_{2}} \\0& 0 \end{bmatrix} x = \begin{bmatrix} \mathbf{b} \\ 0 \end{bmatrix}\]
继续把最下方两个 0 写成行向量的 0:
\[ \begin{bmatrix} A \\0 \end{bmatrix} x = \begin{bmatrix} \mathbf{b} \\ 0 \end{bmatrix}\]
此处已经展现了矩阵分块乘法的雏形,以上例子中当 x 向量不变时,扩展 A 的高度进行乘法是合法的,同样合法的还有:
\( \begin{bmatrix} A \\A \end{bmatrix} x = \begin{bmatrix} \mathbf{b} \\ \mathbf{b} \end{bmatrix}\) 或 \( \begin{bmatrix} A \\cA \end{bmatrix} x = \begin{bmatrix} \mathbf{b} \\ c \mathbf{b} \end{bmatrix}\)
这种扩展在 python 各个矩阵相关包里都没有直接的类似 A_ext=[A;0] 的语法(这里分号表示换行),但也都有各自处理方式:
import numpy as np
import torch
import sympy as sp
# 使用 numpy 创建和扩展矩阵和向量
A_np = np.array([[1, 2], [3, 4]])
b_np = np.array([1, 2])
# 扩展矩阵和向量
A_expanded_np = np.vstack((A_np, np.zeros((1, A_np.shape[1]))))
b_expanded_np = np.append(b_np, [0])
print(A_expanded_np, b_expanded_np)
# 使用 torch 创建和扩展矩阵和向量
A_torch = torch.tensor([[1, 2], [3, 4]])
b_torch = torch.tensor([1, 2])
# 扩展矩阵和向量
A_expanded_torch = torch.vstack((A_torch, torch.zeros(1, A_torch.shape[1])))
b_expanded_torch = torch.cat((b_torch, torch.tensor([0])))
print(A_expanded_torch, b_expanded_torch)
# 使用 sympy 创建和扩展矩阵和向量
A_sym = sp.Matrix([[1, 2], [3, 4]])
b_sym = sp.Matrix([1, 2])
# 扩展矩阵和向量
A_expanded_sym = A_sym.col_join(sp.zeros(1, A_sym.cols))
b_expanded_sym = b_sym.col_join(sp.Matrix([0]))
print( A_expanded_sym, b_expanded_sym)
[[1. 2.]
[3. 4.]
[0. 0.]] [1 2 0]
tensor([[1., 2.],
[3., 4.],
[0., 0.]]) tensor([1, 2, 0])
Matrix([[1, 2], [3, 4], [0, 0]]) Matrix([[1], [2], [0]])
注意自然语言表达和当前矩阵计算库之间还是有一点的间隔,因为从人的视觉理解来看,写成 [A;0]x 似乎是自然的(也可以设计一个新的库使得能够支持这种语法,但可能需要许多区分歧义的推断,比如其中 0 代表什么?是列还是行还是数字,是列的话有多少列?),我就是把 [A;0]x=[b;0] 符号发给 GPT4, 它能够"理解"这中抽象符号,并给出了以上代码:
你认为 [A;0]x=[b;0] 中 0 是什么?
在数学表示 \([A; 0]x = [b; 0]\) 中,\(0\) 通常代表零矩阵或零向量,其具体形式取决于上下文。在这种情况下:
- \(A\) 是一个矩阵。
- \(x\) 是一个向量。
- \(b\) 是一个向量。
- 分号 \(;\) 表示矩阵的垂直拼接。
因此:
- \([A; 0]\) 表示矩阵 \(A\) 的下方拼接了一个零矩阵。这个零矩阵的列数与 \(A\) 相同,行数取决于特定的应用场景,通常是为了匹配 \(A\) 矩阵的列数以保持矩阵乘法的有效性。
- \([b; 0]\) 表示向量 \(b\) 的下方拼接了一个或多个零元素,形成一个新的向量。零元素的数量通常与 \(A\) 矩阵扩展后的行数相匹配。
矩阵的秩和 CR 分解
上一节我们保持 x 不变只对矩阵 A 进行扩展,根据 \( Ax=b \) 那么有:
\[ \begin{bmatrix} A \\ A \end{bmatrix} x= \begin{bmatrix} b \\ b \end{bmatrix}\]
本节则对 x 部分进行扩展,直接获得了矩阵的乘法定义之一 – AB 可以看作用 B 的每一列作为加权系数重新组合 A 的所有列。
\[ A \begin{bmatrix} x & x \end{bmatrix}= \begin{bmatrix} b & b \end{bmatrix}\]
或者:
\[ A \begin{bmatrix} x & y \end{bmatrix}= \begin{bmatrix} Ax & Ay \end{bmatrix}\]
如果 x 和 y 都是单位向量 e1, 那么以上公式右侧就是 [a1,a1] 也就是重复选择了 A 的第一列。 如果 x 是单位向量 e2, y 是单位向量 e1, 那么以上公式右侧就是 [a2,a1], 也就是交换了 A 的两个列,可以看到这里只要对 AB 中 B 矩阵进行适当设置,可以达到对 A 的列进行重排列(洗牌),比如 A 是 3x3 的矩阵,B 是 [e3,e2,e1], 那么 AB 乘法就是对 A 的列进行"逆序"排列。此外,B 的列数可以任意多,因此达到一种类似复制的操作:
\[ A \begin{bmatrix} x & x &x &x &x & e_1&e_2& e_1&e_2 \end{bmatrix}= \begin{bmatrix} b & b& b& b& b& a_{1}& a_2& a_{1}& a_2 \end{bmatrix}\]
现在引入一个重要的概念 – 向量的独立性,如果一组向量相互独立,那么从该组向量里任意选择向量 b 都无法表示成剩余其他向量的线性组合,如果把其他向量排列成的矩阵记成 A 的话,这意味着 Ax=b 无解。
我们把矩阵 A 里相互独立的列向量的最大数量记作是秩(rank)。从以上定义中可以看到,"秩" 这个特征和矩阵里列的顺序应该是无关的,因为独立性这个概念和向量顺序无关,无论 A 的列如何排序, 因为独立性定义中是通过 "任意选择" 这种操作来描述的。这意味着当我们要计算秩或者证明秩的性质时,可以根据计算的便捷性重新排列 A 的列。
有了单位向量、Ax=b 以及秩的概念,就可以对矩阵 A 进行一次"因式分解" 了:
比如 A[e1,e2]=[a1,a2]=A, 因此有 AE=A, E 是标准单位对角矩阵, 这得到了最没有用的分解,相当于 a=1*a.
然而这个思路是一个好的开始,假设 A = [u, v, u+w], 其中 u 和 v 是独立的,也就是 u 无法写成 v 的倍数,同样 v 也无法写成 u 的倍数,而第三列可以被 u,v 的线性组合表示,不独立于其他的列,我们想从 A 中选出尽可能多的独立的列 C,同时用这些独立的列的多次重新组合 – 也就是矩阵乘法 CR 来表示原始的矩阵 A, 那么思路就是:
- 构造一个空矩阵 C 和 R
- 从 A 中先选出第一个非 0 列加入 C, 因为第一个非 0 列相比空矩阵 C 的列肯定是独立的。如果 A 第一列就是非 0, 那么对应的选择向量就是 e1, 将 e1 加入到 R 中。
- 从 A 中找下一个相对 C 来说独立的列 b,也就是使得 Cx=b 无解的列, 将 b 加入到 C 中,如果是第 i 列,那么选择向量就是 ei, 如此循环找出所有独立向量,这些向量组成矩阵 R 。
- A 中剩余的非独立的列都可以表示成 C 的线性组合 Cz,将每个 z 插入到 R 矩阵对应的位置,重新排列组成最终的 R。
对于 A=[u,v,u+w], C=[u,v], \( R = \begin{bmatrix} 1&0&1\\0&1&1 \end{bmatrix} \), R 的前两列表示从 C 里选出相互独立的第一和第二列,第三列表示对 C 的前两列进行求和,因此 A 可以表示成 CR 。
如果 A =[u,u+v,v], 那么 \( A = \begin{bmatrix} u&u+v \end{bmatrix} \begin{bmatrix} 1&0&-1\\0&1&1 \end{bmatrix} \)
这里 R 的前两列还是用 one-hot 向量进行"选择", 因为 u+v 无法被 u 线性组合表示出来,所以它们是相互独立, 第三列则是差分。
当然这种情况,以下分解也是合理的: \( A = \begin{bmatrix} u&v \end{bmatrix} \begin{bmatrix} 1&1&0\\0&1&1 \end{bmatrix} \)
但这不是按照以上描述的(贪心)算法获得的结果,涉及到对 R 的重排列。
展现重排列的更好地例子是 A=[u,2u,v], 由于第二列是第一列的线性组合,因此当 C=[u] 时,我们必须跳过 2u 去找下一个独立的列 v, 当 \(R = \begin{bmatrix} 1&0\\0&1 \end{bmatrix}\) 时再着手处理剩下的非独立列 2u, 并且把 [2,0] 插入到 R 的第二列。
\[ A = \begin{bmatrix} u&v \end{bmatrix} \begin{bmatrix} 1&2&0\\0&0&1 \end{bmatrix} \]
这个算法实际不是"标准"的 CR 分解,CR 中的 C 表示 column, R 表示 row,CR 分解的 的主要作用是证明秩相关的重要定理(下节详细说明),因此标准形式中我们希望 R 的前几列组成一个标准的单位对角矩阵,从而很容易计算出 R 的秩(数学上的规范性常常就是用于展现出特定性质的) 。
尽管如此,还是可以先写出 CR 分解的算法,因为是否标准只和传入以下 CR_decomposition 函数的参数矩阵 A 有关而与算法的核心步骤无关:
import numpy as np
np.set_printoptions(precision=3, suppress=True)
def CR_decomposition(A):
m, n = A.shape
C = np.array([]).reshape(m, 0) # 初始化C为m×0的矩阵
independent_indices = [] # 存储独立列索引的列表
# 首先找出所有独立列并构造C矩阵
for i in range(n):
col = A[:, i:i+1] # 获取A的第i列
if C.shape[1] == 0 or np.linalg.matrix_rank(np.hstack((C, col))) > np.linalg.matrix_rank(C):
# 如果列独立,则将其加入到C中
C = np.hstack((C, col))
independent_indices.append(i)
rank = C.shape[1]
R = np.zeros((rank, n)) # 初始化R为n×n的零矩阵
# 计算非独立列相对于C的系数
for i, col in enumerate(independent_indices):
R[i, col] = 1
for i in range(n):
if i not in independent_indices:
col = A[:, i:i+1]
coeffs = np.linalg.lstsq(C, col, rcond=None)[0]
R[:,i] = coeffs.flatten() # 将系数存储在R的相应位置
return C, R
对代码的说明:
用以下方式检查 Cx=col 是否有解,它实际是分块矩阵一个例子,把 C 和 col 拼接后得到 [C|col], 如果这个矩阵的秩等于 C 的秩,说明 col 可以被 C 线性组合,因此有解,如果无解那么 rank(C|col) 就要大于 rank(C)
np.linalg.matrix_rank(np.hstack((C, col))) > np.linalg.matrix_rank(C)
以上方式只能检查 Cx=col 是否有解,对于有解的情况,要得到具体的 x, 用的是:
coeffs = np.linalg.lstsq(C, col, rcond=None)[0]
这是最小二乘法进行做近似计算,会有一定误差。用 np.set_printoptions 控制精度。
样例测试:
from pprint import pprint
A = np.array([[1, 2, 2], [2, 4, 5], [3, 6, 8]])
pprint(CR_decomposition(A))
(array([[1., 2.],
[2., 5.],
[3., 8.]]),
array([[ 1., 2., 0.],
[ 0., -0., 1.]]))
如果把 A 的第二第三列交换之后传入,就是标准 CR 分解:
pprint(CR_decomposition(A[:, [0, 2, 1]]))
(array([[1., 2.],
[2., 5.],
[3., 8.]]),
array([[ 1., 0., 2.],
[ 0., 1., -0.]]))
注意这样得到的 R 矩阵前 r 列是一个单位对角矩阵 E,可以用分块矩阵表示: R=[E | remain_cols], 这个形状在下一节证明秩性质很有帮助。
A=CR 意味着行空间和列空间的秩相同
CR 分解可以类比于对一个整数进行质数分解,可以看出有哪些关键的乘法因子(比如是不是13 的倍数),但质因数分解有一定应用场景(密码学),而 A=CR 则基本是解释性的而非应用性的,实践中很少用到,正如上节算法里展示的,每一步都要判断 Cx=b 方程是否有解,而 C 和 b 都是在不断变化,因此计算量比较大。
作为理论工具,CR 分解便于更清晰地看到 "rank" 的本质。由于交换列的顺序是不会影响矩阵的秩,因此可以把上一节 提到的例子 A=[u,2u,v] 和交换二三列后的 A'=[u,v,2u] 看作是等价的。
如果严格来写的话, A=CR 可以写成 AP=CR, P 是 permutation 矩阵,如果 P 从左边乘以 A 矩阵(PA),那么就是对 A 的行进行重排列,P 从右边乘以矩阵 AP 则是对 A 的列进行重排列,而重排序的核心是"交换",比如交换二三行/列的 P 矩阵为:
\[ P_{23}=\begin{bmatrix} 1 &0 &0 \\ 0 &0 &1\\0& 1 &0 \end{bmatrix} \]
证明矩阵行空间和列空间的秩相同是 A=CR 分解的核心目的。 矩阵行的 rank 等于列的 rank 性质被 Gilbert Strang 教授称为是 magic of linear algebra 。
- 假设 A 的维度是 (m,n), 秩为 r.
- 首先 CR 分解中 C 的列数在算法设计上就等于 A 的秩 r, 因为我们就是按秩的定义从 A 中选择出前 r 个相互独立的列,剩下的都是可以被这 r 个向量表示的列了。因此 C 是形状为 (m,r) 。
- 接着矩阵乘法的定义使得 R 矩阵的维度必须是 (r,n), 而 R 由于前 r 列是都是 one-hot 向量组成的单位矩阵 E,因此这前 r 列是相互独立的,而 R 的高度又是 r, 因此 R 有 r 个相互独立的列和 r 个相互独立的行.
- 当用 C 的每一行作为线性组合系数去组合 R 的行时,平凡却又神奇的事情发生了,A 的每一行都可以表示成 R 矩阵中 行的线性组合:
- 平凡是因为: A=CR 就意味着,C 的第 i 行乘以 R 会得到 A 的第 i 行
- 神奇在于: A 的行向量组成的线性空间可以通过 R 中的 r 个独立行向量表示,因此 A 的行空间秩也是 r.
- 因此行列秩相等完全来自矩阵乘法定义的内在属性以及秩的定义本身。
这个结论也意味着,如果一个矩阵 A=BC, 那么 A 的 rank 不会超过 B 的第二个维度,或 C 的第一个维度,也就是 rank(BC) <= rank(B), rank(BC)<=rank(C). 这是因为:
- BC 可以看作是用 C 的每列作为系数对 B 的列空间的重新线性组合,所以 A=BC 仍然在 B 的列空间中,因此 A 的秩不会超过 B 的列空间的秩,也就是 rank(B).
- BC 还可以看作是用 B 的每行作为系数对 C 的行空间的重新线性组合,所以 A=BC 仍然在 C 的行空间中,因此 A 的秩不会超过 C 的行空间的秩,而行列空间秩相等,因此 rank(A)<=rank(C)
矩阵乘法的不同视角
前文我们是按照列的线性组合视角来看待 Ax=b 的, 上一节 A=CR 中,用 C 的行作为系数对 R 的行进行线性组合 \( c^{T}R \) 来解释 A 的行空间的秩和列空间秩的关系,这意味着通过不同视角看待矩阵和向量乘法也许能够获得一些重要的洞见。
本节继续发掘矩阵乘法中其他的视角,所有这些视角都来自于 A=BC 中最底层的定义:
\[ A_{ij} = \sum_{k} B_{i,k}C_{k,j} \]
以上定义类比于汇编,而建立在其之上的其他视角则都是对汇编的不同语法的抽象,它们的本质是一致的。
内积视角
\( A_{ij}=B_{i,:}C_{:,j} \) 是以上公式进行一小步抽象的结果,用"内积" 操作封装了按位相乘并求和(注意 \( B_{i,:} \) 表示 B 的第 i 行,这里用类似 numpy 里切片的语法):
矩阵 A 第 i 行第 j 列的值等于矩阵 B 的第 i 行和矩阵 C 的第 j 列的向量的内积。
这类似 numpy 中
import numpy as np
u = np.array([1,2,3])
v = np.array([2,3,4])
sum(u[i]*v[i] for i in range(len(u)))
20
可以封装成:
u.T@v
20
这种封装带来的好处不单单是人类视角下数学符号变得简单,因此可以更方便地进行更复杂的数学推理,对于代码实现来说,还能够把 u 和 v 看作是一个整体对象,硬件层面对这种多数据组合对象有专门的并行处理手段,比如用 SIMD (Single InstructionMultiple Data,单指令流多数据流) 向量指令集来执行真正的乘法,这比 for 循环逐个操作要更加高效,因此这种抽象最终实现了人和机器的"双赢"。
通过内积视角实际可以直接导出前文提到的行和列线性组合视角:
- A 的第 i 行是 B 的第 i 行作为系数时对 C 中所有行的线性组合
- A 的第 j 行是 C 的第 j 列作为系数时对 B 中所有列的线性组合
外积视角
对于 A=BC ,如果 B 的维度是 (m,r), C 的维度是 (r, n), 每个元素的底层表示为 \(A_{ij} = \sum_{k=1}^{r} B_{i,k}C_{k,j} \), 从 \( \sum \) 的上下标可以看出它是由 r 个元素累加而得到的:
- 如果 r=1 ,那 \( A_{ij} \) 就等于 \( B_{i,1}C_{1,j} \), 把 B, C 看作向量话,可以写成 \( B_{i}C_{j} \), 那么 A 的整体结果就是一个列向量 u 乘以行向量 \( v^{T} \),得到一个 rank1 的矩阵(因为每一列都是 u 的倍数,系数是 \( v_{i} \))
- 如果 r=2 ,相当于在 r=1 的基础上,在 B 右侧添加一列,在 C 的下侧添加一行,那么 \( A_{ij} \) 就等于 \( B_{i,1}C_{1,j} + B_{i,2}C_{2,j} \) , 第二元素的意义是,取 B 第 i 行第二列和 C 第 2 行第 j 列相乘,也就是说,相比于第一个元素的计算,计算第二个元素时要在 B 上向右移动一列,在 A 向下移动一行来获取需要的乘数。
因此如果 B 为 \( \begin{bmatrix} \mathbf{b_1} &\mathbf{b_2} \end{bmatrix}\) , C 为 \( \begin{bmatrix} \mathbf{c_1^{T}} \\ \mathbf{c_2^{T}} \end{bmatrix}\), 那么 BC 就相当于 \( \mathbf{b_1} \mathbf{c_1^{T}} + \mathbf{b_2}\mathbf{c_2^{T}} \), 也就是说矩阵乘法可以拆解成 r 个列向量与行向量的外积的和,A=BC 中 A 可以拆分成 r 个 rank1 矩阵之和。
这种分解的一个应用在于:如果我们能够衡量 rank1 矩阵到原矩阵的 A 的"距离", 那么只要从中找出一个距离最近的 rank1 矩阵就可以近似表示 A 矩阵,这在数据科学里非常常见,因为这样我们就可以找出数据里最核心的前几个特征(rank1 矩阵的行空间和列空间)。
SVD 一瞥
SVD 分解使得 A 向量可以写成 \( U\Sigma V^{T} \) 的形式,其中 U 和 V 里都是单位正交矩阵(也就是说 U 的列和 V 的行相乘得到的 rank1 矩阵的"大小"都是一样的),但由于 \( \Sigma \) 是一个对角矩阵,它的对角元素实际是这些 rank1 矩阵的权重,因此我们只需要选择对应权重最大的那个 rank1 矩阵就可以近似原矩阵了。
这些内容会在后文中进一步梳理。
block 视角
前文已经提到过矩阵分块的例子,比如根据 Ax=b 中的 A 进行行扩展:
\[ \begin{bmatrix} A \\A \end{bmatrix} x = \begin{bmatrix} \mathbf{b} \\ \mathbf{b} \end{bmatrix}\]
再对 x 进行列扩展:
\[ \begin{bmatrix} A \\ A \end{bmatrix} \begin{bmatrix} x & x \end{bmatrix}= \begin{bmatrix} b & b\\ b& b \end{bmatrix}\]
此外,把 Ax 看作 A 的列向量的线性组合也是一种矩阵分块的思路,它把 A 按列进行了分块。
本节展示更一般分块矩阵乘法的形式,其核心就是可以把子矩阵看作和普通矩阵中的数一样的对象:
\[ \begin{bmatrix} A &B \\ C&D \end{bmatrix} \begin{bmatrix} X & Y\\ Z& W \end{bmatrix}= \begin{bmatrix} AX+BZ & AY+BW\\ CX+DZ& CY+DW \end{bmatrix}\]
其中每个都是矩阵乘法,因此划分时核心就是保证维度的一致。
要证明以上公式的合理性,一种做法是手动用底层的乘法公式 \(A_{ij} = \sum_{k=1}^{r} B_{i,k}C_{k,j} \) 去展开比较,但这样做是纯粹机械证明的思路,可能对于机器更为擅长,人则容易陷入细节,无法从高层获得"理解"(特定的情形下是可以使用,比如上节中对矩阵乘法外积的视角)。
另一种做法则是从最简单的行列相乘 \( u^{T}v \) 开始,先对向量进行分块,比如假设它们有 5 个元素,那么进行一次分块后,前两个值合并成 u[:2] 向量, 后三个值为 u[-3:] 向量,那么有:
\[ u^{T}v = \begin{bmatrix} u_{:2}^{T} & u_{-3:}^{T} \end{bmatrix} \begin{bmatrix} v_{:2} \\ v_{-3:} \end{bmatrix}\]
说服自己这是可行的,接着扩展到矩阵和向量相乘 Au ,由于 u 已经按 2 比 3 分成两块,那么对 A 的列也进行 2:3 分块成 A[:2], A[-3:], 这里 A[:2] 表示取前两列,那么有:
\[ Au = \begin{bmatrix} A_{:2} & A_{-3:} \end{bmatrix} \begin{bmatrix} u_{:2} \\ u_{-3:} \end{bmatrix}\]
说服自己这是可行的。接着在 A 下方添加多行,把 u 扩展出多列,因此得到矩阵乘法 AB 的 block 形式 …
矩阵分块仍然是一种封装抽象手段,因此同时对人和机器都有好处:
对人带来的便利:
- 通过解题来熟悉基础概念时,一些较大矩阵(比如 6x6 手算起来就很吃力)可能有大量的重复子分块或者有 0 分块,因此通过人眼识别出这种 pattern 进行聚类分块可以简化计算。
- 理论工具:用于证明矩阵的某些性质,比如块对角矩阵的特征向量,或者一些复杂矩阵的秩 (因为一些复杂矩阵可以从小的性质好的块堆叠而成,因此可以用分块来构造"辅助线",比如前文提到的 CR 分解中 R 矩阵可以看作是 [E|cols], 它的秩就是单位对角矩阵 E 的秩)。
对机器带来的便利(最终也是对人的便利):
数学上的分解(decomposition)很容易对应到算法上的分治(divide-and-conquer)
- 现实中计算非常大的两个矩阵的乘法,可以将矩阵分块, 然后每个块放到不同的机器上进行分布式计算,之后再汇总(map-reduce)。
- 更细地算法优化:关注较小矩阵的乘法优化,这也可以看作是机器解题时进行简化计算的技巧, 一个例子是: 【 2022】線性代數 (課程補充):AlphaTensor_用增強式學習 (Reinforcement Learning) 找出更有效率的矩陣相乘演算法_哔哩哔哩_bilibili
子空间,LU 分解和 rank-nullity 定理
前文已经提到了列空间和行空间,但没有正式地说什么是空间和子空间。
(子)空间是向量的集合
所谓空间,在数学中指的就是集合,其中包含了某类对象,线性空间里集合对象是向量,线性说的是,这些对象符合以下"线性"性质:
- 加法和标量乘法符合交换律,结合律以及分配率 (2x3 = 6 条子规则)
- 存在加法 0 对象(单位元),该空间任何对象与 0 对象相加还是得到本身
- 加法逆元的存在性:对于向量空间中的每个向量 u,都存在一个加法逆元 v,满足 u+v = 0
展开后以上实际有 8 条规则(可以有其他等价的规则来描述线性空间,因此不同定义下规则数可能不同),正是这 8 条规则定义了线性空间,本文不讨论为什么选择这些规则,只能说它们是历史打磨出来的"结晶" (它需要满足各种一致性,比如当向量是 1 维的时候可以"退化"到普通的实数运算规则), 本文只是接受它们并按规则"下棋" 。
注意公理中提到了标量乘法,但标量本身不在定义的线性空间中。这就好比说定义一个集合,这个集合是小于 10 的正整数, 但是它们不是 5 和 3 的倍数,那么这个集合就是:
print([x for x in range(1, 10+1) if x%5!=0 and x%3 !=0 ])
[1, 2, 4, 7, 8]
这个集合里是没有 3, 5, 10 的,尽管在定义中提到了它们,也就是说 3,5,10 以及倍数、除法这些对象或运算是预定义好的。
根据这个定义,任何缺乏标量乘法结果的集合都不会是线性空间,比如所有的整数,虽然看上去它本身有 1 对象,0 对象,也符合交换律等,但由于 0.2 不在这个集合里,因此 0.2 乘以整数 1 在整数空间里直接是一个未定义的对象(或者称为标量乘法不封闭),因此 0.2*1 就没法等于 1*0.2, 就像 1 除以 0 也没法等于 2 除以 0 一样,标量乘法也就不符合交换律了。
前文说到到,python 中列表没法作为向量,之前用的例子是 2x2 的嵌套列表和普通长度为 2 的列表乘法会报错:
[[1,2],[3,4]] * [1,0] # error
有了以上公理,我们还可以检查 python 列表加法之间是不符合交换律的:
[1,2,3] + [1,2] == [1,2] + [1,2,3]
False
因此这条规则就足以显示 python 原生的列表没法组成线性空间(尽管列表加法操作是封闭的,其结果也是个列表)。然而,一种最直观的向量的构造是对以上列表的运算进行重载,使得 3 *[1,2] 不是等于 [1,2,1,2,1,2], 而是 [3,6]; 同时使得 [a,b] +[c,d] 不是等于 [a,b,c,d] 而是 [a+b,c+d], 这也就是 numpy 里一维 array 的定义。
span 是通过向量创造子空间的核心方法,很多时候也直接作为子空间的定义,如果 v1 和 v2 是向量,那么 v1 和 v2 的所有线性组合产生的对象的集合被称为 spanning set, 写法为 \( P = \text{Span}\{v_1, v_2\} \) , 它一定是一个线性空间,因为:
- 0 在该空间中;因为它是 \( 0v_1+0v_2 \) 的结果
- 标量乘法是封闭的:根据定义, \( av_{1}+bv_{2} \) 是在 P 中,那么对任意标量 c, \( c(av_{1}+b v_2) = ac v_1 + bc v_2 \), 它还是 v1 和 v2 的线性组合,只不过系数是 ac 和 bc 了。根据这种封闭性继而可以证明其他运算规律是满足的。
- 同样可以证明 P 中向量之间运算规律是封闭的。
注意封闭性是证明的前提,它保证的是某个组合的对象依然存在,从而才进一步去证明交换律等性质(因为交换律前提是通过加法或乘法先构造出一个新对象,如果这个对象都不存在,那么没必要进一步验证),而一旦有了封闭性,其他的性质的证明基本就是一种"底层"展开的验证了。比如定义 [a,b] +[c,d] 为 [a+b,c+d], 只要能证明 [a+b,c+d] 也是在集合里的对象,那么其加法交换律是"天然" 成立的,因为底层的 a+b=b+a 和 c+d=d+c 是符合预定义的标量的交换律的。
最经典的各个维度的线性空间代表是: \[ \mathbb{R}^{n} = P\{e_1,e_2,\dots ,e_{n}\} \]
子空间(subspace)是一个相对概念,它是从某个已经符合线性性质的向量集合(一般就是相应维度 \( R^{n} \))里任意选出一组子集向量然后做 span 操作得到的空间,注意这里核心是选出子集向量后再做 span 得到的结果,单纯的向量空间的子集并不一定是 subspace, 比如一根不过原点的线上的点是二维线性空间 \( R^{2} \)的子集,但它不是子空间,因为不包括 0 向量, 而根据"线性" 的定义, 0 向量必须存在于任何线性空间。
由于一个形状为 (m,n) 的矩阵 A 有 m 个行向量,n 个列向量,那么自然地,可以对这些向量做 span 操作,定义出列空间和行空间:
- 列空间 \( C(A) \) 是 A 的所有列的线性组合结果(spanning set)。
- 行空间 \(C(A^T) \) 是 A 的所有行的线性组合结果。
此外根据 Ax=0 定义出左右零空间:
- (右)零空间 nullspace N(A) 是使得 Ax= 0 的所有 x 组成的空间。
- 左零空间 left nullspace \( N(A^{T}) \) 是使得 \(A^{T}y = 0 \) 的所有 y 组成的空间。
以上实际要证明左右零空间是一个 subspace ,只要证明 0 向量存在且加法和数乘是封闭即可:
- 0 向量在 nullspace, 因为 A0=0 成立。
- 如果 x 和 y 都在零空间,那么 cx 也在零空间,因为 Acx=cAx=0, 同时向量 x+y 也在零空间,因为 A(x+y)=Ax+Ay=0 。而由于零空间里对象本身就是 \( R^{n} \)空间的 子集,因此只要证明了封闭性,其他线性空间的运算规律自然成立。
另外,根据以上定义可以看出 nullspace 里所有向量和行空间中向量是垂直的,而列空间里所有向量和左零空间里所有向量是垂直的,垂直意味着两个向量内积为 0。
线性方程和子空间的关系
如果 A 矩阵形状为 (m,n), 那么对于 Ax=0 和 Ax=b:
- Ax=0 的解在 N(A) 中
- Ax=b 则表示 b 在 C(A) 中
Ax=0 和 Ax=b 解的情况的关系:
- x=0 一定是 Ax=0 的解,说明 nullspace 里一定存在一个 0 向量,这满足线性空间的定义,任何线性空间都应该有 0 向量。
如果 Ax=0 只有 0 解,意味着 N(A) 只有 0 向量,根据独立性定义可以知道 A 的列是线性独立的,rank(A) = n
但是它无法对一般的 Ax=b 解的情况提供特别信息,比如以下矩阵 A 只有 0 解,但随着 b 的不同 Ax=b 可能有解,也可能无解。 \[ A=\begin{bmatrix} 1 &0 \\ 0&1\\0&0 \end{bmatrix} \]
- 如果 Ax=0 有非 0 解,意味着 N(A) 中还存在其他向量,A 的列就是不独立或者说是冗余的,因此 Ax=0 有无数个解,但无数个解中还可以区分不同的子空间的维度。
- Ax=b 可以无解、有唯一解和无数个解,但对于非 0 的 b, 它的解不是在线性子空间中(而是仿射子空间),因此一般不讨论其维度,但它如果有无穷解,Ax=0 肯定也有无穷解,因此可以讨论这种情况下 Ax=0 的解空间。
LU 分解以及同 CR 分解的对比
LU 分解是希望把一个矩阵 A 分解成下三角矩阵(lower triangular matri) L 和上三角矩阵 (upper triangular matrix) U 的乘积,我们 CR 和 LU 的对比中来展示 LU 分解算法过程:
以如下矩阵为例
\[ A=\begin{bmatrix} 0 &0 &2 \\ 1 &2 &1\\2& 4 &3 \end{bmatrix} \]
先进行 CR 分解:首先发现 A 前两列不是独立的,因此可以将 A 乘以一个列交换矩阵,把二三列进行交换再进行 CR 分解
\[ AP_{23}= \begin{bmatrix} 0 &2 &0 \\ 1 &1 &2\\2& 3 &4 \end{bmatrix} = CR = \begin{bmatrix} 0 &2 \\ 1 &1\\2& 3 \end{bmatrix} \begin{bmatrix} 1 &0&2 \\ 0 &1&0 \end{bmatrix} \]
在前文中提到 CR 分解只是来证明行空间的秩和列空间的秩相等,而交换列不影响这个值,但如果要严格进行分解,由于交换矩阵的逆等于其自身,因此 A 的完整分解为: \( A=CRP_{23} \)
接着先看一般的 2x2 矩阵的 LU 分解,我们可以把它写成多个 rank1 矩阵相加的形式:
\[ B = \begin{bmatrix} l_{11} &0 \\ l_{21} &l_{22} \end{bmatrix} \begin{bmatrix} u_{11} & u_{12} \\ 0 &u_{22} \end{bmatrix} = \begin{bmatrix} l_{11} \\ l_{21} \end{bmatrix} \begin{bmatrix} u_{11} & u_{12} \end{bmatrix} + \begin{bmatrix} 0 \\ l_{22} \end{bmatrix} \begin{bmatrix} 0 & u_{22} \end{bmatrix} \]
这里第一个 rank1 矩阵所有元素都是非 0, 而第二个则只有右下角 1x1 矩阵是非 0, 这是一个逐渐 "塌缩" 的矩阵加法,每次加的非零元素都逐渐集中到右下角分块中。
反过来看这意味着,我们可以逐渐把一个矩阵 B 与一个 rank1 矩阵相减:
- 第一次减完后把 B 的第一列和第一行都变成 0 ,得到新的 B
- 在第一次的基础上继续减把第二列第二行也变成 0, 直到都变成 0
我们利用高斯消元的历史过程来完成这些 rank1 矩阵的构造,第一个 rank1 矩阵表示用第一行去消除其他行的第一个列 时所需要的矩阵。
但本例中 A 第一个行第一列为 0 ,也就是其主元(pivot) 不是在第一列,这会导致分解出的 U 不是上三角,因此考虑先进行交换,这和 CR 的动机类似,但由于 LU 分解实际是为了求解 Ax=b 方程,对行进行交换不会影响方程组性质,可以先交换前两行:
\[ A'= P_{12}A=\begin{bmatrix} 1 &2 &1 \\ 0 &0 &2\\2& 4 &3 \end{bmatrix} \]
接着先从 A' 中拆分出第一个 rank1 矩阵,记为 LU1:
\[LU1 = \begin{bmatrix} 1 \\0 \\ 2 \end{bmatrix}\begin{bmatrix} 1 &2 &1 \end{bmatrix} = \begin{bmatrix} 1&2&1 \\0&0&0 \\ 2&4&2 \end{bmatrix} \]
首先 U1 就是 A' 的第一行,且 L 的第一个元素固定为 1, 这样得到的 LU1 的乘积矩阵的第一行一定和 A' 一样,接着 L 的其他元素则是对
以上 LU1 矩阵就可以去对原矩阵进行消元(注意这个消元把第一行本身也给消除了,但被消除的行会被记录在 U 中,因此不会丢失信息,L 中记录的则是每次消元时 pivot 行对其他行的乘法因子),将 LU1 从 A' 中去除之后就会得到第一行为 0, 第一列也为 0 的矩阵:
\[ A'-LU1=\begin{bmatrix} 0 &0 &0 \\ 0 &0 &2\\0& 0 &1 \end{bmatrix} \]
这时候就只需要关注右下角更小的 2x2 矩阵,得到第二个 rank1 矩阵,记为 LU2:
\[LU2 = \begin{bmatrix} 0 \\1 \\ 0 \end{bmatrix}\begin{bmatrix} 0 &0 &2 \end{bmatrix} = \begin{bmatrix} 0&0&0 \\0&0&2 \\ 0&0&0 \end{bmatrix} \]
如果继续消元就是:
\[ A'-LU1-LU2=\begin{bmatrix} 0 &0 &0 \\ 0 &0 &0\\0& 0 &1 \end{bmatrix} = LU3 = \begin{bmatrix} 0 \\0 \\1 \end{bmatrix} \begin{bmatrix} 0 &0 & 1 \end{bmatrix} \]
最终 A' = LU = LU1 + LU2 + LU3:
\[ P_{12}A= LU = \begin{bmatrix} 1 &0 & 0 \\ 0 &1 &0 \\2 &0& 1 \end{bmatrix} \begin{bmatrix} 1 &2&1 \\ 0 &0&2 \\ 0 &0&1 \end{bmatrix} \]
因此 A 最终可以表示为 \( P_{12}LU \)
CR 分解和 LU 分解的异同:
- CR 分解中 C 的列或者 R 的行数等于 rank, 但 LU 分解中 U 会保持和 A 形状一样
- CR 分解中 C 是从 A 的列里直接拿过来的,LU 分解中 U 是从 A 进行高斯消元过程中逐次取出来的。
- CR 分解的 R 是用高斯消元法获得 reduced row-echelon form 形式,只不过不会包括全 0 行,但是从以上例子也看到, CR 分解一般不是用来解方程的,它如果引入列交换就会破坏 CR 分解和解方程之间的对应关系,失去了解方程的意义。
- LU 分解中的 U 是 row-echelon form, 如果继续对 U 从下到上反向消元会得到 reduced row-echelon form 。 L 实际可以看作是各种行基本运算(交换,消元)矩阵的乘积的结果。
- CR 分解可能要借助列交换矩阵来把线性无关的列都放在最左侧,需要右乘交换矩阵,而 LU 分解可能要借助行交换矩阵来把带有 pivot 的行移动到前几行,需要左乘交换矩阵。
求解 Ax=0 以及 rank-nullity 定理
本节用一些例子说明如何求解 Ax=0,而其计算方式也蕴含了 rank-nullity 定理的证明。
先考虑最简单的 A=E 的情况 : \[ \begin{pmatrix} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} x_{1} \\x_{2} \\x_{3} \end{pmatrix} = \mathbf{0} \]
那么可以知道 x 就是 (0,0,0)
接着放松一个变量:
\[ \begin{pmatrix} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 0 \end{pmatrix} \begin{pmatrix} x_{1} \\x_{2} \\x_{3} \end{pmatrix} = \mathbf{0} \]
此时 x1 和 x2 都被限制为 0,但第三行没有主元(pivot) x3 可以取任意值,用 c1 表示,那么可以记为:
\[ \begin{pmatrix} x_{1} \\x_{2} \\x_{3} \end{pmatrix} = c_1 \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} \]
或者写成 x=span{\(\begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix}\)}, 有时候直接写成 x=(0,0,1), 但这里表示的是一个空间而不是单个解。
再考虑 rank=1 的例子
\[ A = \begin{pmatrix} 2 & 1 & 2\\ 4 & 2 & 4\\ 2 & 1 & 2 \end{pmatrix} = \begin{pmatrix} 1 \\ 2 \\ 1 \end{pmatrix} \cdot \begin{pmatrix} 2 & 1 & 2 \\ \end{pmatrix}\]
经过变换可以得到以下 row-echelon form:
\[ \begin{pmatrix} 2 & 1 & 2\\ 0 & 0 & 0\\ 0 & 0 & 0 \end{pmatrix} \begin{pmatrix} x_{1} \\x_{2} \\x_{3} \end{pmatrix} = 0 \]
由于二三行没有主元, x2 和 x3 是自由的,最终 x 写成:
\[ \begin{pmatrix} x_{1} \\x_{2} \\x_{3} \end{pmatrix} = c_1 \begin{pmatrix} -\frac{1}{2} \\ 1 \\ 0 \end{pmatrix} + c_2 \begin{pmatrix} -1 \\ 0 \\1 \end{pmatrix} \]
或者写成 span{(-1/2, 1, 0),(-1, 0, 1)}, 是两个向量的线性组合,还可以写成 X 矩阵的列空间 C(X)。 其中 \( X = \begin{pmatrix} -\frac{1}{2}&-1 \\ 1& 0 \\0& 1 \end{pmatrix} \)
这里得到的一个启示是,如果 Ax=0 的解中有 f 个自由变量,那么矩阵 X 中可以分块划分出一个 f 维的单位矩阵 \( E_{f} \), 由于 f 小于 n, 而 X 的形状是 (n,f), 这使得 X 的秩就等于 f.
因此 Ax=0 的解空间(A 的零空间)的秩 nullity 就等于自由变量的个数,而自由变量的个数实际对应的是消元法得到的 row-echelon 形式矩阵中全 0 行(元全被消掉了的行)的数量,而非 0 行数量就是矩阵 A 的秩 r (因为消元本身是线性组合,没被消掉的就是无法被组合的独立者),这就直接得到了 rank-nullity 定理:
形状为 (m,n) 的矩阵 A 的列数等于矩阵的(列空间)秩加上零空间的秩, n=r+nullity 。
rank-nullity 的证明来自于解方程这个应用,是解方程提供了某种更为直观的意义, 如果要直接按线性空间定义的规则去证明该定理,可能会变得很困难。
特征值和对角化分解
特征值和特征向量是使得 \(Ax= \lambda x \) 成立的 \( \lambda \) 和 x, 这里 A 是方阵,因为如果 A 是 (m,n) 形状,而 m 和 n 不相等,那么 x 的维度是 n, 而 Ax 维度是 m, 无法对齐。
行列式、特征值和 trace 之间的关系
本节通过多项式代数的性质来证明一些和行列式、特征值、trace 有关的等式。 由于去展开多项式是一件机械的底层工作,因此要保持警惕,可以从高层的视角来处理,或者只取部分底层展开的切片,而不是一股脑地全部去陷入细节。
所有特征根的积的性质
根据特征根定义,矩阵 \( A-\lambda I \) 是不可逆的, 也就是它的行列式(det) 为 0
\[ det(A - \lambda I) = 0 \]
等式左侧实际是一个关于 \( \lambda \) 的多项式,最高项次数是 n,因此根据代数基本性质,该方程有 n 个(复数)解,可以写成:
\[ det(A - \lambda I) = (\lambda-\lambda_{1})(\lambda-\lambda_{2})\dots (\lambda-\lambda_{n}) = 0 \]
但此时不能对整个式子去展开, 而是考虑 \( \lambda \) 等于 0 的情况,因为这时候等式左边就是 det(A),可以得到:
\[ det(A-\lambda I) = det(A) = \lambda_{1}\lambda_{2}\dots \lambda_{n} \]
因此 A 矩阵所有特征根的乘积等于它的 det 。
所有特征根的和的性质
首先引入韦达定理,它描述了一元n次方程的根与系数之间的关系,1 元 n 次方程
\[ a \lambda^n + a_{n-1} \lambda^{n-1} + \cdots + a_1 \lambda + a_0 = 0 \]
的所有根的和
\[ \lambda_1 + \lambda_2 + \cdots + \lambda_n = -\frac{a_{n-1}}{a_n} \]
对于 \( det(A-\lambda I) \), 最高项 \( a_{n} \) 为 1, 因此所有特征根的和就是 n-1 次的系数的相反数,根据 det 的计算方式,只有对角线方向的元素的积才对 \( \lambda^{n-1} \) 项有贡献,而这个贡献就是原矩阵对角线上的元素的和(的相反数),因此所有特征根的和就是 trace(A).
对角化和 markov 矩阵
如果方阵 A 的特征矩阵是可逆的,那么 A 可以写成 \( X \Lambda X^{-1} \) , A 能够对角化实际有多个要求:
- 能够有 n 个特征根(这是多项式基本定理决定的,任何一元 n 次方程都有 n 个根),其中 n 个根可能是重复的,比如 (x-3)^2=0 就有两个重复的根 3
- 重复根并不是问题核心,要能够保证特征向量可逆,真正重要的是每个重复 r 次的特征根要能够对应 r 个特征向量。 也就是说,对于重复 r 次的特征根 a, 矩阵 A-aE 的 nullspace 的秩要是 r 才行 (E 是单位对角矩阵)。
不过这里不讨论这些条件的理论证明,因为实践中可以用一些数值算法来检查,A-aE 的零空间秩是否足够等等。
对角化分解和 LU 分解的结果是类似的,可以写成多个 rank1 矩阵相加,额外地,对角化产生的每个 rank1 矩阵有一个权重,即方阵 A 的特征根,它常出现在矩阵求指数的场景中,可以简化计算,比如 markov 矩阵的每一列的和都是 1, 表示状态的转移概率,由于迭代性质,对该矩阵常见操作就是求乘方,即 \( A^{k} \), 这时候对角化写成 \( X \Lambda ^{k} X^{-1} \)。如果特征值都小于 1, 那么 \( X \Lambda ^{k} X^{-1} \) 会趋向于 0 矩阵,而如果只有第一个特征根大于 1, 其他都小于 1, 那么最后会趋向于最大特征根对应的 rank1 矩阵: \( \lambda_{1}X[:,1]X^{-1}[1,:] \).
比如以下 A 矩阵两个特征值是 1 和 -0.3, 而 B 矩阵两个特征值是 0.3 和 0.9, 30 次方之后, B 各个值都接近 0
import numpy as np
from pprint import pprint
from sympy import Matrix
A = Matrix(np.array([[.6, .9], [.4, .1]]))
B = Matrix(np.array([[.6, .9], [.1, .6]]))
pprint(A**30)
pprint(B**30)
Matrix([ [0.692307692307693, 0.692307692307693], [0.307692307692308, 0.307692307692308]]) Matrix([ [0.0607883273127186, 0.182364981833552], [0.0202627757592836, 0.0607883273127186]])
对角化下的矩阵向量乘积 – 基变换视角
第一章我们就提供过一个矩阵乘以向量的定义,对于 Av ,它可以看作是用 v 的系数去对 A 的列进行线性组合。 这种视角有点像是把向量 v 看作是主动的部分,矩阵 A 是被动的,v 去拆解矩阵的每个列然后组成了一个新的向量。
但本节从另外一个角度来看待这个操作,把矩阵 A 看作是主动部分, v 则是被动的, A 像是一个函数或机器,它吸收一个向量 v, 然后对它进行一翻操作,返回一个新的向量 Av, 这个视角需要借助对角化分解,因此这里讨论的是可对角化矩阵与向量乘法的解释。
假设 A 对角化为 \( A= X\Lambda X^{-1} \), X 是一个可逆矩阵,它的 n 个列是线性无关的,记为 X1 到 Xn 而 X 又是形状为 (n,n) 的方阵,因此 X 的列空间实际就是整个 \( \mathbb{R}^{n} \) 空间,所有 n 维向量都可以被 X 的列空间所表示,现在对于任意 n 维向量 v 就可以写成 \( v=c_1X_1+c_2X_2+\dots c_{n}X_{n} \) :
这时候我们可以在对角化后的视角下来看待矩阵和向量的乘法: Av = \( X\Lambda X^{-1}v \) ,它可以分为三步:
\( b=X^{-1}v = c_1X^{-1}X_1+c_2X^{-1}X_2+\dots +c_{n}X^{-1}X_{n} \)
注意 \( X^{-1}X = E \), 因此 \( X^{-1}X_1 = (1,0,..,0)^{T} \), \( X^{-1}X_2 = (0,1,..,0)^{T} \)… 这意味着 \( b=(c_1,c_2, \dots c_{n})^{T} \)
所以 \( X^{-1}v \) 实际是在提取出 v 在 X 基下的系数,也就是把 v 从标准基转换到了 X 作为基的空间中。
- \( b' = \Lambda b = \Lambda X^{-1}v \) : 这是对 v 在 X 基下的各个轴的系数进行缩放。
- \( X b' = X \Lambda X^{-1}v \) :将缩放后的系数加权到各个 X 列向量上,这实际是又把向量重新转回到了标准基空间中。
因此如果 A 可以对角化,那么 A 乘以向量 v 可以解释成,A 先把 v 拉进一个以特征向量 X 为基的新的时空中(由于 X 是还是 n x n 形状 ,因此没有降维也没有升维),在这个时空里对 v 的形态进行拉伸压缩,然后再推回到原来的时空。
对第一步的额外说明: 由于 \( X^{-1}v \) 实际是把 v 在标准基里的坐标转成以 X 列作为基的坐标。那么对于任意的可逆矩阵 B 乘以向量 v 就是把 v 从标准基空间转换到了以 \( B^{-1} \) 的列作为基的空间,矩阵乘法本身就可以看作是基变换,但前提是要理清变换到哪个空间。
再比如,如果某个向量 v 中的值不是标准基的系数,而是 C 为基下的系数,那么要获得它在 B 为基的坐标,可以先把 v 转到标准基下,再转到 B, 也就是 \( B^{-1}Cv \)
实对称矩阵和谱定理
S(对称矩阵) and Q(单位正交矩阵) 被 Gilbert Strang 教授称为是 the kings and queens of linear algebra
对称矩阵的性质优势在于:
- 所有特征值都是实数,这样特征值可以按大小进行排序,分清主次,后文优化问题会关心它们。
- 所有特征向量都可以构造成正交形式(因此相互独立),如果继续变成单位向量,那么就会获得 orthonormal 的特征向量,这类特征向量组成的特征矩阵为 Q, 满足 \( Q^{T} = Q^{-1}, Q^{T}Q=E\) ,翻个身就能得到逆矩阵。
二者结合起来可以得到: 所有对称矩阵都可以写成 \(S = Q \Lambda Q^{T} \) 形式; 这也称为谱定理 (Spectral Theorem) 。
以上性质都是从 "对称" 扩展出来的。
先证明 S 的特征矩阵的列之间是正交性质:
矩阵对称意味着 row space 等于 column space, 而 row space 和 null space 是正交的,因此对称矩阵的 column space 和 null space 是正交的。假设 S 存在两个特征根 x 和 y, 且 \( Sx=\lambda x \) , \( Sy=\alpha y \), 此时分成三种情况:
\( \lambda ,\alpha \) 相同都等于 a, 那么说明这是重复特征根,那么 x,y 都在 S-aE 的 nullspace 中,因此我们可以在这个子空间选择出相互正交的特征向量,这是 Gram-Schmidt 正交化发挥作用的场景,正交化的结果是 QR 分解,这里 Q 是正交单位矩阵, R 是一个上三角矩阵,这里不进行推导,直接给出 qr 分解代码。
import numpy as np B = np.array([[3, -9, 4], [6, 10, -8], [-4, 6, -41]]) Q, R = np.linalg.qr(B) print(Q) print( R)
[[-0.38411064 0.64297729 0.66260035] [-0.76822128 -0.62065169 0.15693166] [ 0.51214752 -0.44874457 0.73234775]] [[ -7.81024968 -1.15233192 -16.38872063] [ 0. -14.6857799 25.9356499 ] [ 0. 0. -28.63130979]]
- 如果 \( \lambda \) 不是 0, \( \alpha \) 是 0, 说明 y 在 S 的 nullspace, 而 x 在 S 的 column space,前文说到对称矩阵的 nullspace column space 正交,于是 x 和 y 正交
- 如果 \( \lambda \) 和 \( \alpha \) 都不是 0 且二者不相等, 那么根据 \( Sx=\lambda x \) 可以得到 \( (S-\lambda I)x=0 \), 因此 x 在 \( S-\lambda I \) 矩阵的 nullspace 中。而为了和 y 建立起联系,可以构造出式子 \( (S-\lambda I)y \) , 它等于 \( (\alpha-\lambda)y \) , 也就是说 y 在 \( S-\lambda I \) 的 column space 中,而该矩阵也是对称的,那么 y 同样在 \( S-\lambda I \) 的 row space 中,因此 y 和在 nullspace 中的 x 是垂直的。
所以对称矩阵的所有不同根的特征向量之间都是垂直的。
再来证明 S 的特征根为实数:
根据 \( Sx=\lambda x \), 两边乘以 x 的共轭转置向量, 那么有 \( \bar{x}^{T}Sx=\lambda \bar{x}^{T}x \) ,这种情况下,只要证明 \( \bar{x}^{T}Sx, \bar{x}^{T}x \) 都是实数即可,对于 \(\bar{x}^{T}x \) ,即便 x 向量里存在复数 a+bi ,它和共轭复数的乘积也是 \( a^{2 }+b^{2} \) ,因此一定是实数。
接着证明 \(x^{T}Sx \) 结果为实数,用一个 3x3 矩阵作为示例:
\[ \begin{pmatrix} \bar{x_{1}} &\bar{x_{2}} &\bar{x_{3}} \end{pmatrix} \begin{pmatrix} S_{11} & S_{12} & S_{13} \\ S_{12} & S_{22} & S_{23} \\ S_{13} & S_{23} & S_{33} \end{pmatrix}\begin{pmatrix} x_{1} \\x_{2} \\x_{3} \end{pmatrix}\]
先对前两个矩阵相乘后结果: \[ \begin{pmatrix} \bar{x_{1}}S_{11} +\bar{x_{2}}S_{12}+\bar{x_{3}}S_{13} & \bar{x_{1}}S_{12} +\bar{x_{2}}S_{22}+\bar{x_{3}}S_{23} & \bar{x_{1}}S_{13} +\bar{x_{2}}S_{23}+\bar{x_{3}}S_{33} \end{pmatrix} \begin{pmatrix} x_{1} \\x_{2} \\x_{3} \end{pmatrix}\] 继续相乘得到的结果是:
\[ \bar{x_{1}}x_{1}S_{11}+(\bar{x_{1}}x_{2}+ \bar{x_{2}}x_{1})S_{12} \cdots \]
由于对称性,在非对角线上的元素都出现了两次并且 \( S_{ij} \) 的系数对应的是 \( \bar{x_i}x_j \) 和 \( \bar{x_j}x_i \), 而这些系数如果继续用 a+bi, c+di 的一般复数形式来表示,展开后发现也都是实数。 因此只要对称矩阵里都是实数,那么特征根也是实数。
补充说明:
- 实对称矩阵中,"对称" 决定了特征根是实数以及相互正交,”实“ 决定了特征向量是实数,但如果不是 "实" 的,实际上包含复数的对称矩阵(Hermitian matrix,满足 \( A^{T}=\bar{A}, 而不是 A^{T} =A \))的特征根也是会是实数,但特征向量可能是正交的复向量。
- 实数非对称矩阵的特征根可以是复数。
- 对于现实中的数据,如果某个矩阵非常接近对称,比如 [1,0.000001; 0, 1], 但这种表层数据上的近似对称不会使得它的特征向量近似垂直,它们特征向量之间的角度可能是任意的。
对称矩阵 S 乘以向量 v, 从分解的视角来看是 \( Q\Lambda Q^{T}v \) ,这和前文提到的对角化视角类似,都是先把 v 转到 Q 的空间,沿着各个主轴方向拉伸或压缩后返回到原空间,唯一差别就是 Q 是正交单位矩阵,正交基变换会保持原向量的长度和夹角不变,这是因为:
- 对于长度: \( \|Qv\| = (Qv)^{T}Qv=v^{T}Q^{T}Qv=v^{T}v \)
- 对于角度: 由于 Qu 的长度 Qv 不变,因此计算它们的内积就可以反应出角度了: \( (Qu)^{T}(Qv) = u^{T}Q^{T}Qv=u^{T}v \)
因此 u,v 经过 Q 变换后,二者之间的角度仍然等于变换前两个向量的角度,长度也保持不变。而一般的特征矩阵 X 的变换可能会改变向量的长度和夹角。
对称矩阵 S 另外的好处就是只要得到了特征矩阵 Q, 求转置获得逆矩阵非常方便。
双空间的基变换和单空间线性变换
正交单位矩阵二维线性变换类型
前文提到,当特征矩阵 Q 是正交单位矩阵时,正交基变换会保持原向量的长度和夹角关系不变,因此这种变换相对单纯,比较容易进行命名和展示,在二维空间中,这类变换有:
旋转
满足 \( QQ^T = I \), 其 det 是 1 。注意如果是正交单位矩阵,其行列式 det 要么是 1 要么是 -1 。
反射(翻转)
同样满足 \( QQ^T = I \), 但它的 det 是 -1
比如 permutation 矩阵 \( P = \begin{pmatrix} 0 & 1 \\ 1 & 0 \\ \end{pmatrix} \) 它会交换坐标轴, 但向量之间的相对关系是不会改变的。
因为我们不希望(纯粹的)旋转和反射影响变换前后向量的长度,而正交单位矩阵 Qx 的长度仍然是 x 的长度,符合该预期。
对于这两种变换的组合:
- 旋转矩阵乘以旋转矩阵还是旋转矩阵;
- 反射矩阵乘以反射矩阵是旋转矩阵;
- 旋转矩阵乘以反射矩阵等于反射矩阵;
此外正交矩阵与投影也密切相关,如果一个矩阵 P 满足 PP=P, 那么它就是投影矩阵,因为对 x 进行两次或者多次投影,结果应该都是 Px, 因此要满足 PPx=Px ,想象一下一个三维空间的对象在地面的影子,这个影子继续投影到地面,应该还是影子本身,也就连续投影和一次投影应该是等价的。而 P= \(QQ^T\) 就满足这个性质,这里 Q 可以不是方针,而是它的列都是互相垂直的,且 \( Q^{T}Q = E \)
一般基变换和线性变换对比
从 A 对角化分解后分步乘法来看,A 乘以 v 先是做两个空间之间的的基变换,接着进行拉伸,最后又做基变换回到标准空间。其中基变换涉及两个空间,但拉伸又是在同一个空间里,总的结果就是 Av 的结果还是标准空间中,因此很多时候我们说的 A 乘以 v 是 A 对向量 v 进行了线性变换,这种说法一般默认是在同一个空间下的操作(前提是 A 是可对角化的方阵,对于其他情况 Av 也是线性变换,但可能涉及升维或降维,因此不在同一个空间了)。
本节以二维空间中的一个例子来理清基变换和同一个空间中线性变换的区别,如下图 (a) 所示,向量 \( v=\begin{pmatrix} 2 \\ 1 \\ \end{pmatrix} \) 是标准基(i 和 j)下的坐标(也称系数):
假设某个矩阵 A 的特征向量是分别是 (1,0) 和 (1,1), 那么特征矩阵及其逆矩阵就是:
\[ X = \begin{pmatrix} 1 & 1 \\ 0 & 1 \\ \end{pmatrix}, X^{-1} = \begin{pmatrix} 1 & -1 \\ 0 & 1 \\ \end{pmatrix} \]
把 X 看作是基的话,相当于把 y 轴折叠到 45 度位置,假设 A 的特征根是 (1,2) 那么 \( A = \begin{pmatrix} 1 & 1 \\ 0 & 2 \\ \end{pmatrix} \)
Av 在对角化后看待乘法的三个步骤如下:
\( b=X^{-1}v = (1,1)^{T} \) :
注意有两种看待 (1,1) 的方式,分别对应图 (b) 和图 (b2):
图 (b) 是基变换视角,它提取出 X 的列作为基的情况下 v 向量的系数。因此图中把 X 的第二列 X2 作为基画在标准空间中,这个时候向量 b 等于 X2+X1, 这对应图中平行四边形表示, (1,1) 代表了 X 两个列的组合系数。这个视角来看,我们只是拿了另外一个坐标系(一个 45 度角的教案尺)叠加在标准坐标系上(因此 j 轴浅灰色仍然存在),去重新测量了 v 向量 在新坐标系下的系数,这种情况下 b 和 v 是相同的。
另外系数是根据新的坐标系的长度来确定的,比如 X2 向量在标准基下长度是 \( \sqrt{2} \), 但不能以此作为 X2 的系数,而是取 1 。如果 X 是单位正交矩阵,那么原坐标系里的尺度和新坐标系是相同的, 图中的平行四边形会变成矩形。
- 图 (b2) 是线性变换的视角。我们把 (1,1) 看作是原始标准坐标系里的一个向量,在这个视角下, \( X^{-1}v \) 是对 v 向量沿 i 轴方向做压缩。
\( b' = \Lambda b = \Lambda X^{-1}v = (1, 2)^{T}\)
如图 (c) 和 (c2) 所示,都是对第二个轴拉伸了 2 倍,这里的倍数都是要以各自坐标轴为准,对于图 (c) 是以 (1,1) 向量为准,图 (c2) 则以 j 向量为准。
\( X b' = X \Lambda X^{-1}v = (3,2)^{T}\)
图 (d) 展示了这个结果,由于它最终回到了标准坐标系,因此 X2 坐标轴不再需要了。
总结图中的两条路径异同:
- a->b->c->d 经历的过程是:基变换,拉伸,基变换。我们用一个辅助的尺子(坐标系)去换了一个角度看待 v 向量,取出它在另外一个视角下的分量不会对向量进行任何变换,只有按照新尺子下的刻度进行缩放时会改变原始 v 向量,再通过标准坐标系读取出新向量的刻度就得到了最终的 Av; 因此这个过程本质上只对向量做了一次变换,其他时候看作是信息提取。
a-b2->c2-d 经历的过程是:v 向量始终在标准坐标轴下从一个形态变换到另外一个形态,先横向拉伸变换,再纵向拉伸,最后旋转拉伸;因此这个过程做了三次变换。如果 A 是对称矩阵,那么特征矩阵 X 是单位正交的 Q, \( Q\Lambda Q^{T}v \) 变换中 第一次和最后一次变换中不会出现拉伸,只会有旋转或(换轴)翻转,这是一种更加"干净" 的动作分解,这种情况下,我们更倾向于用线性变换视角来看待矩阵和向量的乘法,而不是基变换视角。
下一个小节则用例子说明。
实对称矩阵的线性变换
本节完全用线性变换的视角来可视化对称矩阵和向量的乘法,以下 A 是对称矩阵,求出对角化分解中需要的矩阵:
import numpy as np
import matplotlib.pyplot as plt
A = np.array([[3, 2],
[2, 3]])
eigenvalues, eigenvectors = np.linalg.eig(A)
# 构造对角矩阵D和正交矩阵Q
D = np.diag(eigenvalues)
Q = eigenvectors
Q
[[ 0.70710678 -0.70710678] [ 0.70710678 0.70710678]] [[5. 0.] [0. 1.]]
这里 Q 的行列式为 1, 因此这是一个旋转矩阵。
np.linalg.det(Q)
0.9999999999999999
为了可视化变换过程,先取单位圆上各个方向的向量,对其中一个向量用红点表示,以突出旋转效果,并且求出变换的三个步骤:
# 生成单位圆上的点
theta = np.linspace(0, 2 * np.pi, 100)
circle_points = np.array([np.cos(theta), np.sin(theta)])
# 变换步骤
Q_T_v = Q.T.dot(circle_points) # Q^T*v
D_Q_T_v = D.dot(Q_T_v) # DQ^T*v
Q_D_Q_T_v = Q.dot(D_Q_T_v) # QDQ^T*v
然后绘制出各个步骤,第二幅图是原图顺时针旋转的结果,然后在标准 x 轴方向进行了拉伸,拉伸长度是特征值 5, 接着又按照相同的角度逆时针旋转回去(因为 \( Q^{T} \) 是 Q 的逆操作)。
D
array([[5., 0.],
[0., 1.]])
画图代码
# 绘制变换过程
plt.figure(figsize=(12, 4))
# 原始单位圆
plt.subplot(1, 4, 1)
plt.plot(circle_points[0, :], circle_points[1, :], 'gray')
plt.scatter(circle_points[0, 10], circle_points[1, 10], color='red') # 特殊点标记
plt.title('Original Unit Circle')
plt.axis('equal')
# Q^T*v
plt.subplot(1, 4, 2)
plt.plot(Q_T_v[0, :], Q_T_v[1, :], 'gray')
plt.scatter(Q_T_v[0, 10], Q_T_v[1, 10], color='red') # 特殊点标记
plt.title('After Q^T*v')
plt.axis('equal')
# DQ^T*v
plt.subplot(1, 4, 3)
plt.plot(D_Q_T_v[0, :], D_Q_T_v[1, :], 'gray')
plt.scatter(D_Q_T_v[0, 10], D_Q_T_v[1, 10], color='red') # 特殊点标记
plt.title('After DQ^T*v')
plt.axis('equal')
# QDQ^T*v
plt.subplot(1, 4, 4)
plt.plot(Q_D_Q_T_v[0, :], Q_D_Q_T_v[1, :], 'gray')
plt.scatter(Q_D_Q_T_v[0, 10], Q_D_Q_T_v[1, 10], color='red') # 特殊点标记
plt.title('After QDQ^T*v')
plt.axis('equal')
plt.tight_layout()
plt.show()
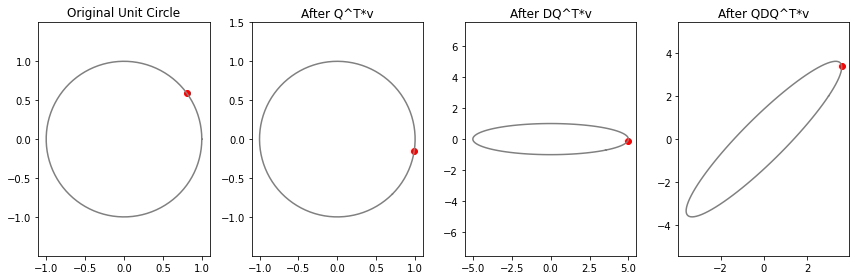
这里展示了,对称矩阵对向量进行线性变换的过程实际就是找到特征向量对应的各个方向进行拉伸或压缩。
正定矩阵、 Cholesky 分解
正定矩阵是在实对称矩阵基础上,继续添加一个好的性质:特征值都是正数。它被 Gilbert Strang 教授誉为 the center of applied mathematics。而半正定则是特征值里可以包括 0 的实对称矩阵。
正如线性代数里的各个操作都有非常多的视角(意味着很强的通用性,比如矩阵乘法可以从行列相乘也可以从列行相乘的角度来看),"正定" 也是如此,有 5 种等价定义(或者用于检查矩阵是否正定的方式):
- 所有特征值都大于 0
可以从能量的角度来定义,正定矩阵是指对于任何非零向量 x,其能量 \( x^T S x \) 都大于 0 的矩阵, 都是"正能量" 。
这个性质的一个推论是,正定矩阵的对角线上不能有非正数,因为一旦出现, \( x^{T}Sx \) 中的的某个 \( x_{i} \) 平方项系数为负数,此时可以把这个 \( x_{i} \) 设置为很大的值,因此这一项就是一个很小的负数,其他 \( x_{i} \) 设置为 0, 那么得到的结果就是负的,这可以用来快速排除某些不是正定的矩阵。
对于 \( x^{T}Ax \) 展开的函数来说,A 叫作二次型矩阵,如果 x 里都是变量,那么 \( x^{T}Ax \) 可以看作是一个函数,此时 A 和该函数二阶导数 Hessian 矩阵是同样的,如果该矩阵是正定的,该函数就是一个凸的钵状,因此有最小值。
- 每一个左上角子矩阵的 det 都大于 0
- 消元后得到的每一行的 pivot (第一个非 0 元素)都大于 0
对于任意矩阵 A, \( A^{T}A \) 是半正定对称矩阵。对称很好证明,直接在高层对其进行转置得到的还是这个公式本身。 半正定也容易证明 \( x^{T}A^{T}Ax = (Ax)^{T}(Ax) = \mid Ax\mid ^{2} \ge 0\)
因此如果某个矩阵 S 可以分解成 \( A^{T}A \) 形式, 那么 S 就是半正定的。
这个式子同时表明,如果 A 的列是相互独立的(注意 A 可以不是方阵),那么只有 x 为 0 时 Ax=0 才成立, 因此 \( A^{T}A \) 就是正定的,这是构造正定的方法也是判断是否正定的一种方法。
最后一个判断条件引出了 Cholesky 分解: 用一个 2x2 实对称非正定矩阵来说明:
\[ S = \begin{bmatrix} 1 & 2 \\ 2 & 1 \end{bmatrix} \]
对于矩阵\(S\),我们有:
- 第一个主子式(左上角的元素):\(1 > 0\),满足正定的条件。
- 矩阵\(S\)的行列式:\(1*1 - 2*2 = -3\),不是正的。因此 S 不是正定矩阵。
对 S 进行 LU 分解得到:
\[ S = LU = \begin{bmatrix} 1 &0 \\ 2 &1\end{bmatrix} \begin{bmatrix} 1 &2 \\ 0 &-3 \end{bmatrix} \]
继续分解得到:
\[ S = \begin{bmatrix} 1 &0 \\ 2 &1\end{bmatrix} \begin{bmatrix} 1 &0 \\ 0 &-3\end{bmatrix} \begin{bmatrix} 1 &2 \\ 0 &1 \end{bmatrix} \]
这是 \(LDL^T\) 的形式,所有对称矩阵进行 LU 分解后都可以得到这种形式,而如果 S 是正定的,那么 D 对角矩阵所有元素就是正的,因此开平方后可以得到 \( L\sqrt{D}\sqrt{D}^{T}L^{T} = A A^{T} \), 这被称为 Cholesky 分解。
我们来验证为什么以上非正定的 S 无法进行 Cholesky 分解,如果强行去对 S 里的 D 求根号会出现复数:
\[ S = \begin{bmatrix} 1 &0 \\ 2 &1\end{bmatrix} \begin{bmatrix} 1 &0 \\ 0 &\sqrt{3}i\end{bmatrix} \begin{bmatrix} 1 &0 \\ 0 &\sqrt{3}i\end{bmatrix} \begin{bmatrix} 1 &2 \\ 0 &1 \end{bmatrix} \]
如果要把 \( \sqrt{D} \) 强行分配到两个 L 中,那么:
\[ S = \begin{bmatrix} 1 &0 \\ 2 &\sqrt{3}i\end{bmatrix} \begin{bmatrix} 1 &2 \\ 0 &\sqrt{3}i \end{bmatrix} \]
这虽然是 \( AA^{T} \) 或 \( A^{T}A \) 形式,而 \( x^{T}Sx \) 看上去是 \( (Ax)^TAx \) 的模长平方形式,似乎不会为负数, 但结果确实是 -1 ,这是因为对于带复数的矩阵,模长的平方应该对应的是 \( (Ax)^{\star}Ax \), Cholesky 应该写成 \(S=A A^{\star} \), 这里 \( A^{\star} \) 是 A 的共轭转置。
对于正定矩阵,我们还有另外一种分解 S 为 \( A^{T}A \) 的方法,即直接进行对角化得到 \( Q\Lambda Q^{T} \), 由于 \( \Lambda \) 都是正的,因此可以直接把它的平方根分配到 Q 中,只不过对于 Cholesky 分解,其乘法因子 A 是上三角矩阵的形式,但不是正交的。
最后,正定矩阵乘以向量 v 与实对称矩阵乘以向量的差别就在于,转换到正交基 Q 空间后,由于特征值都是正数,因此只会对各个轴进行拉伸或压缩,但不会变换方向。
\( AA^T \) 的形式和意义
到目前为止,除了 LU 分解和证明 rank-nullity 之外借助了解方程时移动行列不影响方程结果这个"外部意义", 其他时候我们都是在"按规则办事",也就是按照线性空间的定义、秩的定义、乘法加法的定义来推进,数学本身都是纯形式的学科,其意义来自于两部分:
- 形式本身的带来的意义:比如加法交换律,独立性,对称性,正交
- 但真正在应用时,我们需要外部的意义注入到形式系统中去,并选择意义一致的规则进行推理。 比如由于知道交换行不会影响方程的解(但显然改变了每一个列向量的具体值),所以可以引入一个行交换矩阵,然后讨论这个矩阵的可逆性等内部意义, 从而形式化推演出更多数学性质,再把这个性质映射回到外部世界。
例如,到目前为止,我们并不知道 \(AA^T \) 和 \( A^{T}A \) 代表什么,但它在形式系统内部的意义有很多:
- 根据矩阵乘法规则,如果 A 形状是 (m, n), 那么 \(AA^T \) 和 \( A^{T}A \) 形状分别是 (m,m) 和 (n,n), 都是方阵。
- 根据转置的规则可以推理得到其转置还是自己,因此它们是对称矩阵。
- 半正定
- 如果 Ax=0 那么 \( A^{T}Ax=0 \) ,因此 A 的特征根也是 \( A^{T}A \) 的特征根,反过来,如果 \( A^{T}Ax=0 \), 那么 \( x^{T}A^{T}Ax = ||Ax||^{2} = 0 \), 因此 Ax=0, 这说明 \( A^{T}A \) 的特征根也是 A 的特征根,所以二者的 nullspace 是相同的,也就是它们的 nullity 也相同,而它们的列数都是 n, 根据 rank-nullity 定理,它们的 rank 也是相同的,即 \( r(A^TA) = r(A) \), 同样的方法可以证明 \( r(AA^T) = r(A^{T}) \) ,由于行列空间 rank 相等的性质,这四个 rank 都相等: \( r(A^TA) = r(A) = r(AA^T) = r(A^{T}) \)
- trace(\( A A^{T} \)) = trace(\( A^{T}A \)) 且都等于 A 的所有元素的平方和(也称为 F 范数)
外部意义的例子:
引入概率中的意义:协方差矩阵
用以下简单例子来说明,假设有两个人的身高和体重特征,单位分别是米(m)和千克(kg), 第一行为身高,第二行为体重:
import numpy as np features = np.array([[1.7, 1.8, 1.65], # 身高 [65, 75, 68]]) # 体重
先对一个特征计算均值并中心化数据,该操作来自于统计中样本协方差的定义,接着 \( A A^{T} / (n-1) \) 就代表了协方差矩阵,这里仍然是统计学赋予的意义。
mean_centered_features = features - features.mean(axis=1, keepdims=True) # 构建协方差矩阵 cov_matrix = mean_centered_features @ mean_centered_features.T / (features.shape[1] - 1) cov_matrix
array([[ 0.006, 0.317], [ 0.317, 26.333]])有了协方差矩阵后才进入到了线代的空间,上文提到的内部意义就都出现了,比如它是对称的,半正定的,可以进行对角化等等,之后要做的是在推理中努力对齐和发掘统计世界和线性空间里各自的意义。例如任何人都可以对协方差矩阵进行 Cholesky 分解,CR 分解,LU 分解等等,但这些分解的结果在统计上有什么解释吗?如果有话那便建立了两个领域的桥梁。而后文会介绍,对协方差矩阵进行 SVD 分解出的结果被发现可以有统计上的解释,和去噪、压缩概念建立联系,其应用就变得宽广起来,SVD 的内涵也获得了扩充。
- 图论中意义: graph Laplacian, 本文不做说明
范数和优化问题的引入
"距离"和优化问题的引入
到目前为止,我们更多是做不同功能的矩阵分解,就像用不同的方式拆卸一个玩具,我们只在基变换的时候提到过向量模长 \( \|x\| =x^{T}x \), 这是最常见也是默认的向量长度的计算方式,但衡量长度的指标并不是唯一, 就像现实中两个地方可以用不同交通方式来衡量距离一样。 模长就像面向对象里某个具体的表示长度的类, 而它继承了一个叫作 "范数" 的抽象类。
范数可以看作是一种把"立体"的向量、矩阵数据结构映射成单一个非负实数的操作或函数,并符合以下两个额外性质:
- 标量 c 缩放性质: \( \|cv\|= c\|v\| \)
- 三角不等式: \( \|u+v\| \le \|u\| + \|v\| \)
和线性空间的定义类似,尽管这是一种典型的抽象的数学定义(只描述性质,而不说它是什么,编程里叫作 duck typing, 维特根斯坦则声称世界是事实的总和而不是事物的总和),但它实际是给向量空间中的对象赋予一种人类能够感知到的意义 – 距离,比如对于一个 100x100 的矩阵列构成的 100 维列空间,其中的向量代表什么我们几乎无法想象, 然而如果能够给这些向量赋予一个大于等于 0 的实数,那么至少提供了一个非常具体的感知它们的视角(引入了几何直观), 我们可以比较大小(这是实数"实" 的优势),谈论相似性等等,由于不为负数,因此可以讨论最小值,优化问题等等。 而以上两个性质直接也对应了欧几里得平面上人们对长度的直觉。
注意以上两个性质决定了范数是一个凸函数,凸函数 f 满足:对于任意 \( x_{1} \) , \( x_{2} \) 以及在 0 到 1 之间的系数 \( \theta \) ,满足:
\[ f(\theta x_{1}+(1-\theta)x_{2}) \le \theta f(x_{1})+(1-\theta)f(x_{2}) \]
以上公式里的运算符和范数性质里的运算符几乎重叠,有标量 \( \theta \) 从某个函数里提取到函数外,有两个对象的加法从范数(函数)内提取到范数(函数)外的不等式。因此把 f 替换成范数符号,把 c 替换成 \( \theta \) 和 \( 1-\theta \) 就可以从范数性质直接得到凸函数性质。
凸函数的性质转换到更具体的感知上就是:
- 局部最小就是全局最小
- 只有唯一的全局最小值
向量的范数
\( \|v\| \) 默认是 \( l^{2} \) 范数,或写成 \( \|v\|_{2} = \sqrt{|v_1|^{2} + |v_1|^{2} +\dots |v_n|^{2} } \), 一般提到模长或向量长度就是指该范数。
而一般的 \( l^{p} \) 范数为 \( \|v\|_{p} = \sqrt[p]{|v_1|^{p} + |v_1|^{p} +\dots |v_n|^{p} } \), 这里 \( |v_{1}| \) 是绝对值。
注意 p 要大于等于 1, 否则这个函数是非凸的,因此不能称为范数。
一个有趣的点是,当 p 趋于无穷的时候, \( \|v\|_p = \left( \sum_{i=1}^{n} |x_i|^p \right)^{\frac{1}{p}} = \max({|v_{i}|}) \) (通过在第二个式子提取出 max 值后可以证明)
另外,尽管 p 小于 0 时以上定义的函数不能称为范数,但我们可以定义 \( \|v\|_{0} \) 是 v 向量中非 0 元素的个数(注意这不是 p 趋向于 0 所得到的具体值,因为 p->0 时以上式子没有极限)
有了向量范数定义,我们就可以在求解线性方程后添加一些最优化的约束,比如求解 Ax=b 有时候会有得到多个解,这时候现实中可能要找到是其中符合某个最优条件的解:
- 模长最小的解:最小化 \( \|x\|_{2} \) 同时满足 Ax=b
- 比如最稀疏的解:找出 Ax=b 中非零元素最少的解,这个约束对应的实际 \( \|v\|_{0} \) ,但它又不是凸的,不太好解,不过由于 L1 范数的结果天然是稀疏的,因此可以用 L1 这个凸范数的限制来求解这个非凸问题。
\( l^{2} \) 范数的另外优点在于,它可以用向量内积来表示, \( \|v\|^{2}_{2} = \|v\|^{2} = v^{T}v \), 继而可以扩展到两个向量之间的内积和范数的关系: \( v^{T}w = \|v\|\|w\|\cos \theta \)
内积是接受两个输入的函数,更多描述的是两个向量的关系,它的计算非常直接,其内涵和标准的矩阵或向量之间乘法是一致的,可以将其称为线性操作。此外,内积和范数的关系引出了一个新的"几何直观" – 向量角度,这使得有可以带着更多意义来看待矩阵和向量之间操作。
内积和 L2 范数之间的关系 \( \|v\|^{2}=v^{T}v \) 还可以扩展出一个新的范数: \( v^{T}Sv \), 这里 S 是正定矩阵,这被称为 S norm, 根据 Cholesky 分解,S 可以写成 \( S=A^{T}A \), 因此 \( v^{T}Sv = (Av)^{T}(Av)\), S 正定使得 A 的列是独立的,因此 S norm:
- 是对原始向量进行线性变换后得到的长度
- 可以扩展到两个向量的关系, \( v^{T}Sw = (Av)^{T}(Aw)\) 表示对两个向量做线性变换后的某种距离。
- 在前文正定矩阵一节还提到,这种形式也称为能量,如果 v 和 w 中元素是变量,那么它的结果是一个二次型函数
爱因斯坦提出四维时空,需要在该空间定义一个新的距离, Lorentz 给出以下结果,爱因斯坦采纳了:
\[ \mathbf{v}=(x,y,z,t), \|v\|^{2}= x^{2}+y^{2}+z^{2}-c^{2}t^{2} \]
其中 c 是光速,这可以看所是一个假的 S-norm, 其中:
\( S =\begin{bmatrix}1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0\\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & ic\end{bmatrix} \)
之所以是假的,是因为 S 不是正定,其中有复数。
函数的范数
如果把有限维向量扩展到无限维空间向量,它们的模长和有限维空间向量模长定义类似,只不过需要取极限,例如:
\[ \|a\|_{l^2} = \sqrt{\sum_{i=1}^{\infty} |a_i|^2} \]
继续推广,可以把函数看作是线性空间,因为对于函数 f 和 g, 标量 c 和 d, 满足 cf+dg 也是函数。
对于函数空间的模长计算是把加法变积分,对于函数\(f(x)\),其\(L^2\)范数(或模)在区间\([a, b]\)上定义为:
\[ \|f\|_{L^2} = \left( \int_{a}^{b} |f(x)|^2 dx \right)^{1/2} \]
前提是满足其结果是一个有限值,它衡量函数变化的振幅或者能量
矩阵的范数
继续扩展到矩阵范数,它也是一个实数,满足类似向量范数的以下性质:
- 标量 c 线性缩放性质: \( \|cA\|= c\|A\| \)
- 三角不等式: \( \|A+B\| \le \|A\| + \|B\| \)
额外地还包括:
- \( \|AB\| \le \|A\| \|B\| \)
为什么有这个性质?一种解释是,矩阵可以看作是一种线性变换,是一个操作或函数,它作用在一个向量上时,会改变它的长度和方向,因此矩阵的范数体现的是变换的能力,但由于对不同向量进行变换会得到不同的结果,因此我们往往要取这个矩阵的最大能力,也就是:
\[ \|A\| = \max_{x \ne 0}\frac{\|Ax\|}{\|x\|} \]
注意,根据 max 的含意,这个式子表明了 \( \|Ax\| \le \|A\| \|x\|\), 从而有 \( \|ABx\| \le \|A\| \|Bx\| \le \|A\| \|B\| \|x\| \) 因此
\[ \frac{\|ABx\|}{\|x\|} \le \|A\| \|B\| \]
左侧对任何 x 都成立,因此对于其最大值 \( \|AB\| \) 也成立,这就可以得到 \( \|AB\| \le \|A\| \|B\| \)。
\( \|x\|, \|Ax\| \) 可以是前文对应的任何具体的向量范数,例如如果是 Lp 范数,我们就得到了矩阵的 p 范数
\[ \|A\|_{p} = \max_{v \ne 0}\frac{\|Ax\|_{p}}{\|x\|_{p}} \]
由于线性缩放性质,对 x 乘以或除以一个系数不会影响等式右边的值,因此可以把 x 的范数限制为 1, 那么矩阵 A 的范数可以是:
\[ \|A\| = \max_{\|x\|=1} \|Ax\| \]
这表示矩阵 A 对 x 变换前后能够达到的最大拉伸能力。
典型的矩阵 \(p\)-范数有对应的”封闭解“:
- 1-范数:矩阵 A 的列中最大的 L1 norm 值
\[ \|A\|_1 = \max_{1 \leq j \leq n} \sum_{i=1}^{m} |a_{ij}| \]
- 2-范数(谱范数):最大奇异值(后文介绍)
\[ \|A\|_2 = \sqrt{\lambda_{\text{max}}(A^TA)} =\sigma_1 \]
- \(\infty\)-范数(行和范数):矩阵 A 的行中最大 L1 norm 值
\[ \|A\|_\infty = \max_{1 \leq i \leq m} \sum_{j=1}^{n} |a_{ij}| \]
除此之外,符合矩阵范数约束的其他范数还包括:
- Frobenius范数:把矩阵展平成向量后求 Lp norm,
\[ \|A\|_F^{p} = \sqrt[p]{\sum_{i=1}^{m}\sum_{j=1}^{n} |a_{ij}|^p} \]
一般情况 \( \|A\|_{F} \) 指的就是 Frobenius 2 范数。
每种范数衡量的是矩阵变换能力的不同方面,例如,2-范数(或谱范数)对应了奇异值,因此衡量矩阵作为线性变换在任何方向上的最大拉伸能力。Frobenius 范数提供了一种衡量矩阵“整体大小”的方式,类似向量模长。
类似向量的 "L0 范数" 不是范数一样,矩阵的 Spectral Radius 也不是范数,它定义为矩阵 A 中最大的特征根的绝对值,用于衡量 A 矩阵求指数的收敛情况,这在 markov 链中已经提到过。
SVD 分解
SVD 相比其他分解的优势
对称正定是应用数学中矩阵最好的性质,这类矩阵有非常干净利落的分解方式,这是设计的产物,问题是现实中可以出现各种矩阵,比如不是对称的,也不是方阵。 因此我们需要一种更通用的分解方式。
SVD 核心是把任意矩阵 A (按重要度)分解成了多个 uv 相乘的 rank 1 矩阵的和,那么前文提到的 CR, LU, \( X\Lambda X^{{-1}} \) 不都可以表示成多个 rank1 矩阵相加吗? SVD 的特别之处在哪里?
- 首先 SVD 适用于任何形状的矩阵,不单单是方阵,也不需要是对称甚至正定,因此它通用性非常强,这是相比 \( X\Lambda X^{-1} \) 的一大优势。
- CR, LU 分解确实可以把一个矩阵转成多个 rank1 矩阵的加法,但它们分解出的各个 rank1 矩阵没有一定的"区分度",我们更多是去关注这些分解后矩阵的某个切片性质,例如 rank ,因此它们更多是用于证明某些定理的工具,比如 CR 分解用于证明行空间秩等于列空间秩,LU 分解用于证明 rank-nullity 定理。
- SVD 将矩阵分解成 \( U\Sigma V^{T}\), 它和实对称矩阵的分解 \( Q\Lambda Q^{T} \) 很像, U 和 V 也都是正交矩阵,但 U 、 V 不是相同的矩阵,维度也不同, U 的形状是 (m,m), V 的形状是 (n,n), \( \ \Sigma\) 形状则是 (m,n), 甚至不是方阵,它只是一个局部的对角矩阵(需要用到分块的方法)。 然而这个局部的对角矩阵有很好的性质,它的值都是正数(正定性质,一般对称矩阵对角化得到的特征值还可能是负的),因此可以按大小排序(U,V 也同时重新排列),而由于 U 和 V 又都是正交单位矩阵,它们的 L2 范数都是 1,因此 rank1 矩阵的权重完全就由奇异值来决定, 对于以范数作为衡量矩阵之间距离的应用场景(比如视觉上图片压缩,PCA),我们可以适当抛弃一些权重很小的 rank1 矩阵来近似原矩阵,称为低秩近似。
SVD 分解的标准算法
我们希望把任意一个形状为 (m,n) 的矩阵都拆解成 A = w1C1+w2C2+w3C3.. 其中 Ci 是 rank1 矩阵, w1 是非负的实数(后称奇异值),从大到小排序,这种形式也出现在对角化 \( X\Lambda X^{-1} \) 或 \( Q\Lambda Q^{T} \) 的 rank1 展开中。因此 SVD 分解可以写成)\( A = U\Sigma V^{T} \) (这里 U V 是正交矩阵)
或者:
\[ AV=U\Sigma \]
该式子直接就体现出 V 中列向量和 U 中列向量的关系: \( Av_{i} =\sigma_{i}u_{i} \), 因此只要求出 V 就可以找出 U 。
此外,从线性变换的角度来看,该式子表明 A 对 V 里所有正交的向量转换之后,仍然得到一组正交的向量 U.
再回到 \( A=U\Sigma V^{T} \), 求转置有 \( A^{T}= V\Sigma^{T}U^{T} \), 两式分别进行左右相乘得到 \( AA^{T} = U\Sigma \Sigma ^{T}U^{T} \), \( A^{T}A=V\Sigma ^{T}\Sigma V^{T} \), 前文证明过,这两个矩阵都是半正定的,因此要么特征根为 0 要么为正。(出现 0 的解释:如果 A 是 mxn 形状, m>n 时 \( AA^T \) 一定是不可逆,因此存在 0 特征根)
而以上分解形式和正定矩阵分解形式 \( Q\Lambda Q^{T} \) 是一样的,因此 U 实际就是 \( A A^{T} \) 的特征向量,V 是 \( A^{T}A \) 的特征向量,奇异值则是 \( A A^{T} \) 或 \( A^{T}A \) 的特征根的平方根。(\( A^{T} Ax=\lambda x \) 两边乘以 A 就得到 \( AA^{T}Ax=\lambda Ax \) ,因此它们特征根都是 \( \lambda \))
一般我们只需要计算出 \( A ^{T}A \) 的特征向量和特征根就可以得到 V 和 \( \Sigma \),通过 \( Av_{i} =\sigma_{i}u_{i} \) 再计算出 U 。
对于得到的分解,其形状如下:
但是,由于 \( A A^{T} \) 的秩和 A 的秩是相等的(因为前者是 A 的列的组合,)因此奇异值只有 r 个,r 是 A 的秩,它可能小于 n, 所以 \( \Sigma \) 中可能有纯 0 列或纯 0 行,这时候可以用到分块矩阵的性质,把 U V 和 \( \Sigma \) 简化:
图中黄色部分都可以被抛掉, U 的形状是 (m,r), \( \Sigma \) 形状是 (r,r), \( V^{T} \) 形状是 (r, n) 。
本节介绍的是 SVD 分解的理论计算方法,这个方法可谓利用了前文所讲到的大部分知识,包括对称矩阵的性质、特征根分解、正交化、矩阵分块等等,它具有通用性和数学上的美感,证明了任何矩阵都可以分解成三个更为基础、性质更优越的矩阵,从而给原矩阵提供了非常多的视角。
但要注意的是,现实应用中的矩阵可能会非常大,并且有缺失值或其数值本身就是不精确搜集的,从计算角度看,以上提到的 SVD 分解算法是比较低效的,更多还是一种理论工具。因此 numpy 或者其他包对 svd 的实现往往是用迭代的近似数值计算方法,类似的,近似求解 Ax=b 引出了最小二乘等各类数值方法。
SVD 分解下的矩阵向量乘法
前文我们讨论了矩阵和向量相乘在多种分解下的视角,包括对角化 \( X\Lambda X^{-1} \), 谱定理下的分解 \( Q\Lambda Q^{T} \), 这些对矩阵 A 都有一定的条件要求,比如需要可以对角化、对称或者正定。而 SVD 则非常通用,因此可以从一般视角来分解性地理解矩阵和向量乘法,前文提到过分解后的两种视角:
- 基变换-线性拉伸-基变换
- 在同一个坐标系下进行三次不同线性变换
对于 SVD 来说, Ax 写成 \( U\Sigma V^{T} x \) ,由于 U 和 V 都是单位正交矩阵,因此用线性变换视角更容易理解:
- \( b=V^{T}x \) 对 x 进行旋转/翻转
- \( b'= \Sigma b \) 对 b 进行拉伸(如果 \( \Sigma \) 不是方阵,那么某些维度直接压缩到 0, 也就是降维或者在升到高维空间,但许多维度为 0)
- \( Ax= U b' \) b' 在进行旋转/翻转
如果用基变换视角,由于 U 和 V 是不同的,无法回到标准空间,因此解释起来会有点混乱:
- \( b=V^{T}x \) 对 x 进行正交基变换,变换到了 V 的列向量为基的新空间。
- \( b'= \Sigma b \) 对 V 为基空间下的向量 b 进行拉伸缩放
- \( Ax= U b' \) 将缩放后的 b 再进行正交基变换,映射到 \( VU^{T} \) 为基的空间,这似乎没什么意义,因此不好解释。
方阵对角化和奇异值分解对比
对于矩阵 \( A=\begin{bmatrix}0 & 2 & 0 \\ 0 & 0 & 3 \\ 0 & 0 &0\end{bmatrix} \), 它的特征根都是 0 (三重特征根),但它只有一个特征向量, 因此无法对角化,如下:
import numpy as np
from pprint import pprint
from sympy import Matrix
A = Matrix(np.array([[0, 2, 0], [0, 0, 3], [0, 0, 0]]))
pprint(A.eigenvals())
pprint(A.eigenvects())
{0: 3}
[(0, 3, [Matrix([
[1],
[0],
[0]])])]
但是它可以进行奇异值分解:
\( A^TA =\begin{bmatrix}0 & 0 & 0 \\ 0 & 4 & 0\\ 0 & 0 &9\end{bmatrix} \), \( AA^T = \begin{bmatrix}4 & 0 & 0 \\ 0 & 9 & 0\\ 0 & 0 &0\end{bmatrix}\).
因此奇异值就是 3 和 2, 特征向量就是标准的单位向量,3 对应的是 [0;0;1], 2 对应的是 [0;1;0] 对应的 V 和 U 矩阵分别为:
\( V = \begin{bmatrix}0 & 0 \\ 0 & 1\\ 1 & 0 \end{bmatrix}\) \( U = \begin{bmatrix}0 & 1 \\ 1 & 0\\ 0 & 0 \end{bmatrix}\)
因此 reduced SVD 分解为
\( A = \begin{bmatrix}0 & 1 \\ 1 & 0\\ 0 & 0 \end{bmatrix} \begin{bmatrix}3 & 0 \\ 0 & 2 \end{bmatrix} \begin{bmatrix}0 & 0 & 1 \\ 0 & 1 & 0 \end{bmatrix}\)
它实际等于 2 个 rank1 矩阵的和:
\( A = 3 \begin{bmatrix}0 \\ 1\\ 0 \end{bmatrix} \begin{bmatrix}0 & 0 & 1 \end{bmatrix} + 2 \begin{bmatrix}1 \\ 0\\ 0 \end{bmatrix} \begin{bmatrix}0 & 1 & 0 \end{bmatrix}\)
如果足够大胆(当然这个例子不太好),可以抛弃掉最小的那个奇异值,然后用 \( \)
\( 3 \begin{bmatrix}0 & 0 & 0 \\ 0 & 0 & 1\\ 0 & 0 &0\end{bmatrix}\) 去近似 A 。
另外,实对称正定矩阵 S 的特征根和奇异值是一样的,其对角化形式也就是 SVD, 例如对角化为 \( S=Q\Lambda Q^{T} \), 那么 \( SS^{T} = S^{T}S = Q\Lambda^{T} Q^{T}Q\Lambda Q^{T} = Q\Lambda^{T} \Lambda Q^{T} \), 因此奇异值就是特征根,而 U 和 V 都等于 Q。
优化视角下的 SVD: Eckart-Young 定理
具体证明参考书本,这里只是给出结论,因为对理解用 SVD 进行压缩的应用有帮助。
该定理是说,对于任何 rank 小于等于 k 的矩阵 B, 都满足:
\( \|A-B\| \ge \|A-A_{k}\| \)
其中 \( A_{k}=\sigma_{1}u_{1}v^{T}_{1} + \sigma_{2}u_{2}v^{T}_{2} +\dots + \sigma_{k}u_{k}v^{T}_{k} \), 也就是对 A 进行 SVD 分解后取最大的 k 个非 0 奇异值所对应的 rank1 矩阵的和,注意这个矩阵的秩是 k, 因为它可以写成是 \( U_k\Sigma_{k}V_{k}^{T} \), 而 \( U_{k} \) 是 k 个独立且正交的单位列向量, \( \Sigma_{k}V_{k}^{T} \) 是各行独立且正交(加权后不是单位行向量了)的形状为 (k,n) 的矩阵,那么 \( A_{k} \) 就可以表示成 n 个独立的系数对正交列进行加权的结果,因此它的秩就是 k 。
另外,以上的范数适用于 L2 和 Frobenius norm 等满足酉不变性 (unitarily invariant) 的范数,即满足 \( \|Q_{1}AQ_{2}^{T}\| = \|A\| \) 。
该定理表明的是,SVD 分解出的前 k 个 rank 1 矩阵的和就是最接近原始矩阵 A 的 rank 小于或等于 k 的矩阵了。
也就是说,如果找一个 rank 为 k 的低秩矩阵近似 A, 那么直接做 SVD 取前 k 个 rank 1 的和就是最优解。
现实应用中要考虑的实际是 "近似" 的意义,比如说,如果要压缩一张图片,那么 L2 范数真的可以作为人肉眼区分两张照片是否相似的距离吗?显然如果把一张图片旋转 1 度,人眼看上去可能几乎没有差别,但前后两张图的 L2 norm 会有很大差别。也就是说,可能进行了一次 SVD 压缩,但人眼上较重要的信息却也丢失了。
优化视角下的 SVD: 最大拉伸能力
前文介绍过,矩阵 L2 范数的定义如下 \[ \|A\|_2 = \max_{x \neq 0} \frac{\|Ax\|_2}{\|x\|_2} = \sqrt{\lambda_{\text{max}}(A^TA)} =\sigma_1 \]
它的结果就是 A 矩阵的最大奇异值,但并没有推导这个结论,也没有对其进行扩展,比如其他的奇异值是如何获取的?
本节则描述这个问题的求解,将其写成内积的形式后的优化目标为 \( \|A\|_{2}^{2}=R=\frac{x^{T}A^{T}Ax}{x^{T}x} =\frac{x^{T}Sx}{x^{T}x} \)
这个公式被称为 Rayleigh Quotients ,我们的目标就是找到 R 的最大值, x 求导并置为 0, 可以得到:
\[ \frac{\partial R}{\partial x} = 2Sx(x^{T}x)-x^{T}Sx(2x) = 0 \]
这就等于求解 \( Sx=Rx \), 也就是说, R 要获得最大值,那么 x 就会是 S 的一个特征向量,R 本身就是其特征根,因此 x 取最大特正根所对应的特征向量时,R 也会最大,R 的最大值就是 \( A^{T}A \) 的最大特征根, 也就是 A 的最大奇异值的平方。
再回到几何意义视角: 矩阵 L2 范式衡量的是 x 被 A 线性变换后,模长的最大变化比例,这里 x 的长度可以取为 1, 因为 \( \|cx\|=c\|x\|, \|Acx\|=c\|Ax\| \), 任何对 x 的缩放都会被约分掉。因此奇异值分解中最大的奇异值就是表示 A 对一个单位向量线性拉伸后最大饿长度。
现在,假设 S 最大特征根对应的特征向量是 v1, 那么由于下一个特征向量和 v1 是垂直的,因此可以把优化问题描述成, 在 \( x^{T}v_1=0 \) 情况下,找出 R 的最大值,由于限制条件,x 不可能继续是 v1, 因此只能是其他的特征向量。可以用拉格朗日乘子法来求解带约束的优化,但以下用换基的视角来看待这个问题:
首先假设 \( S=A^{T}A \) 的特征根从大到小排列是: \( \lambda_{1}, \lambda_{2}, \dots ,\lambda_{n} \) , 对应的特征向量是 \(v_1,v_2, \dots v_{n} \), 由于 S 对称矩阵,因此特征向量都是正交的,此时任何向量 x 都可以写成: \( c_{1}v_{1}+c_{2}v_2 + \dots +c_{n}v_{n} \)
那么 Rayleigh Quotients 中分母 \( x^{T}x = c_1^{2} +c_2^{2} + \dots c_{n}^{2}\), 分子: \[ x^{T}Sx = \lambda_{1}c_1^{2} +\lambda_{2}c_2^{2} + \dots \lambda_{n}c_{n}^{2} \le \lambda_{1}c_1^{2} +\lambda_{1}c_2^{2} + \dots \lambda_{1}c_{n}^{2} \]
因此 \( R \le \lambda_{1} \), 而当 \( c_{1}=1 \) 或任意常数,其他 \( c_{i}=0 \) 时就可以取到上限 \( \lambda_{1} \), 因此这里比较容易就得到了最大值。
现在是,我们已经获得了使得 R 最大的 v1=(1,0,…,0), 想要找除此之外的下一个令 R 最大的 x, 由前文求导数方法可知,它必须是和 v1 垂直的,也就是 \( x^{T}v_1=0 \) ,这意味 x 中 c1 必须是 0, 那么优化对象变成了: \[ \frac{\lambda_{2}c_2^{2} + \dots \lambda_{n}c_{n}^{2}}{c_2^{2} + \dots c_{n}^{2}} \]
这是相同的子问题,因此得到 c2=1, 其他 \( c_{i} \) 为 0, 依次类推,可以得到每个不同级别的最大值,分别对应的是奇异值的平方。
PCA: 统计意义的注入
PCA 的动机
PCA 是 Principal component analysis 的缩写,其中 Principal component 被称为主成分,其目的是找到数据中方差最大的方向,这个方向代表的是数据的一个新特征。
下图是二维场景下线性回归和 PCA 目标的对比,首先可以看到数据总体的趋势是从左下到右上角的,因此方差最大的方向应该大致也是如此。
- 线性回归希望找到一条直线,使得所有点沿着 y 方向(类似 L1 距离)到直线的距离的平方和最小
- PCA 希望找到一条直线,使得所有数据点到直线的最小距离(类似 L2 距离)的平方和最小。(后文将解释该目标和最大化方差的关联)

由于对数据点进行总体的上下或左右平移并不会影响这条直线的方向,因此 PCA 做的第一件事情是对数据中心化,把数据点平移到以坐标原点为中心,这样我们只需要找一条过原点的直线(这需要展开距离公式来证明中心化后直线是过原点的),从而可以用 y=ax 来表示直线,而过原点的直线可以用单位向量 w 来表达,如下图所示,这样能够更方便地计算点到直线的距离:
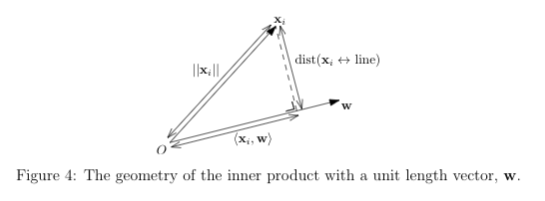
上图中 w 就是要找的目标变量,它是单位向量,因此 PCA 优化目标就是:
\( \text{argmin }_{||w||=1} \frac{1}{m}\sum_i^m \text{dist}(x_{i}, \text{line})^{2} \)
而由于 \( x_{i} \) 是每个数据点对应的向量,它的长度是常数,最小化一个固定斜边长度的直角三角形的直角边,就等于最大化其另一条直角边,因此目标可以写成(这里需要平方,因为点积结果可能会使负数):
\( \text{argmax}_{||w||=1} \frac{1}{m}\sum_i^m (x_i^{T} \cdot w)^{2} \)
该式子的另外一个解释就是最大化所有数据在 w 方向上投影的样本方差(严格来说还要乘以 m/(m-1), 但这只是常数,可以不考虑),因此几何上的最小化点到直线距离的平方和与统计上的最大化数据样本方差的目标一致了。
注:以上两幅图都来自 Lecture 7: Understanding and Using PCA
样本协方差矩阵的出现
继续整理优化对象 \( \text{argmax}_{||w||=1} \frac{1}{m}\sum_i^m x_i^{T} \cdot w \) ,如果 X 是一个形状为 (m,n) 的矩阵,其中 m 是样本个数, n 是特征数量(比如身高,体重),那么 \( x_{i} \) 就是其中的一行,以上式子又可以写成:
\[\operatorname*{argmax}_{||w||=1} (Xw)^T(Xw) = \operatorname*{argmax}_{||w||=1} w^TX^TXw \]
这里出现了多个熟悉的形式:
- \( S=X^{T}X \): 由于 X 已经归一化,因此这实际是数据的协方差矩阵(再乘以 m-1)
- 优化的目标则是 优化视角下的 SVD: 最大拉伸能力 一节中提到的 Rayleigh Quotients
由此,我们已经可以知道:
- 计算 PCA 的一种方法就是对 X 进行 SVD 分解并找出对应奇异值最大的(前几个)特征向量了。
另一种计算方法是对协方差矩阵 S 进行特征分解,找出最大的特征根对应的特征向量。
由于前文说过,对称矩阵对向量的乘法可以看作是在特征向量方向进行对应的特征根大小的缩放,而以上 推导表明协方差矩阵的第一个特征向量就是方差最大的方向,这意味着如果把协方差矩阵作为一个线性变换矩阵, 它可以把均匀的数据转换到接近原数据的分布下。或者说,协方差矩阵刻画了数据样本的大体轮廓。
以下代码把协方差矩阵线性变换的几何意义和统计意义联系起来。首先生成如下数据,并计算协方差
import numpy as np
import matplotlib.pyplot as plt
# 生成数据
hessian = np.array([[2 1]
[1 5]])
np.random.seed(0)
x = np.random.normal(0, 1, 1000)
y = x + np.random.normal(0, 1 + np.abs(x), 1000) # 增加的噪声随x的绝对值增大而增大
data = np.vstack([x, y]).T
cov_matrix = np.cov(data.T)
print(cov_matrix)
[[0.97520967 0.91185835] [0.91185835 4.1953532 ]]
接着我们生成各个方向的单位向量,画出来就是一个单位圆,再用协方差矩阵对这个单位圆上的向量进行线性变换:
theta = np.linspace(0, 2 * np.pi, 100)
circle = np.array([np.cos(theta), np.sin(theta)])
# 应用协方差矩阵的线性变换
transformed_circle = cov_matrix.dot(circle)
结果如下:
plt.figure(figsize=(10, 5))
# 左图:原始数据散点图
plt.subplot(1, 2, 1)
plt.scatter(data[:, 0], data[:, 1], alpha=0.6)
plt.title('Original Data Scatter Plot')
plt.axis('equal')
# 右图:协方差矩阵的线性变换
plt.subplot(1, 2, 2)
# 单位圆
plt.plot(circle[0, :], circle[1, :], 'b', label='Unit Circle')
plt.plot(transformed_circle[0, :], transformed_circle[1, :], 'r', label='Transformed by Covariance Matrix')
plt.title('Linear Transformation by Covariance Matrix & Unit Circle')
plt.legend()
plt.axis('equal')
plt.tight_layout()
plt.show()
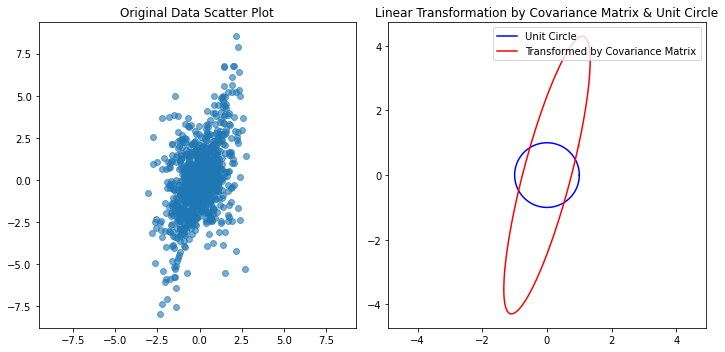
协方差矩阵把圆的轮廓变成了数据的大致轮廓
PCA 涉及的方法、场景和局限
从前文看到,要比较清晰地理解 PCA ,我们需要以下知识:
- 矩阵投影:因为 PCA 是做降维投影
- 矩阵求导和拉格朗日乘子: Rayleigh Quotients 最优化中涉及
- 协方差矩阵:最后变成了求该矩阵的最大特征根和特征向量
- 特征分解/SVD: 优化问题中发现解出了矩阵特征根的形式
但也不是必须掌握这些底层知识的所有细节,就好比没有必要了解计算机汇编你也能用 linux 写文章一样,何况现实中计算 pca 不一定用 svd, 计算 svd 也不会是用特征分解的方式,而更可能是一些高效的迭代算法, 底层的细节被刻意封装以使得更多人能够方便使用:
import numpy as np
X = np.random.randn(10,4)
u,s,v = np.linalg.svd(X.T @ X)
u.shape, s.shape, v.shape
u
最后再强调 PCA 和线性回归(LR)的相似和差异,以突出其应用场景和局限:
它们都可以看作是在对数据做线性拟合
- PCA 拟合最小投影距离,它的(第一次投影)结果是要找到一个新的基,把所有数据"挤压" 到投影面上,投影完后我们还需要对这个维度进行解释,赋予该维度意义(可以是现实中已有的,也可以是抽象的)。
- LR 是在现有的基的维度上最小化平方距离,把所有数据挤压到一个已经有意义的维度上,因此它的重点是得出现有维度(特征)之间的关系,对这个关系进行解释,而不是对维度进行解释。
使用场景上,PCA 会用于:
- 降维:压缩
- 去噪:可能奇异值小的维度大部分是噪声,这时候可以根据奇异值衰减程度来删除最小的若干个维度
- 展示样本的线性子结构: 比如取前两个主成分的话,就可以用来对高维数据进行二维可视化 一个例子是对欧洲基因数据做二维 PCA, 可视化之后发现其分布很像是一个欧洲地图(这种能够从主成分中找出真的高层意义的研究是比较有解释性价值的)。
不适用 PCA 的场景则有:
- scaling/normalizing 没有选好: PCA 对单位太敏感,如果没有选好归一化方式,可能得不到好的结果
- 非线性结构数据: 例如某个数据的分布是在球面上,那么各个维度的方差大小类似,线性降维一定会丢失重要信息。
非正交的线型结构数据: 由于 PCA 分解出的是正交的轴,但如果某些数据的主要的可解释性特征不是正交的,那么分解出来之后的那几个维度也不具备解释性。
如果只求 top 1 的轴,一般都会有解释意义,但由于之后的轴都是相互正交,故事就很难继续往下讲了。
- 高方差噪声混合的数据:如果数据的噪音是由一个高方差的分布产生,那么 PCA 直接保留了噪音而抛弃了数据真正的结构