用 python matplotlib 画递归图
SICP 中 picture language 及更多分形的 matplotlib 实现
修改历史
- 大修,用自己的话描述了一遍 picture language 的原理,以及更多实现分形图的方法说明
- 原题 "sicp 中 picture language 的 matplotlib 实现" 放到 subtile
本文是对 sicp 的 2.2.4 节 picture language 的理解和 python 实现,个人发现网络上能找到的 python 实现大多都是基于 python turtle 包, 这不适合在 jupyter notebook 或者 emacs org babel 里运行,但我更喜欢在这类交互式环境下试验代码, 因此尝试用 matplotlib 作为绘图的底层实现。
语言和魔法
书本里对 picture language 的介绍是自上而下的,比如最先给出代码是:
(define wave2 (beside wave (flip-vert wave)))
(define wave4 (below wave2 wave2))
它告诉你可以用 flip-vert 将一张图片(被编码成 painter 对象)翻转,也可以用 beside 把两张图片左右排列,用 below 将两张图片上下排列。
有了这些接口函数之后,马上就可以定义递归形式的代码:
(define
(right-split painter n)
(if (= n 0)
painter
(let ((smaller (right-split painter (- n 1))))
(beside painter (below smaller smaller)))))
以此绘制出书本里给出的递归样式的图片。
在 SICP 的语境下,以上出现的 painter, beside, below, flip-vert 就是一个新语言的基本组成,由于其封闭性质,也就是 beside, below,flip-vert 都是接收(一个或两个) painter 对象作为参数,再返回 painter 对象,这和 scheme 里的 cons 运算是类似的, cons 可以接收 list 作为对象同时返回一个 list:
(cons 0 (cons 1 ())) ;; (0 1)
因此 Scheme 中能够对 list 进行什么样的递归操作,就能对 painter 进行类似的操作(只要 painter 的实现又是基于 scheme 基础语法的,比如是一个 list 或一个函数),这使得我们得到了一门可以“描述”图片递归模式的语言,它“寄生”在 scheme 中。
比如可以用高阶函数形式写出以下类型的代码:
(define
(square-of-four tl tr bl br)
(lambda (painter)
(let ((top (beside (tl painter) (tr painter)))
(bottom (beside (bl painter) (br painter))))
(below bottom top))))
这种抽象的动机可能来自于:实践中发现经常对画布平分为四块,然后把原图缩小并进行一定类型的转换后放到这些小区域中,有时候是对左上角图片上下翻转后再递归,有时候是左右翻转后再递归,那么 “一分为四再进行 X 转换后递归” 就是一种模式,将该模式用 scheme 语言描述出来就得到以上函数,把 flip-vert 等作为参数传给 square-of-four 就能构造出在四个角度方向不断翻转的递归图片。
(define
(flipped-pairs painter)
(let ((combine4 (square-of-four identity flip-vert
identity flip-vert)))
(combine4 painter)))
可以看到,在我们不知道 painter 到底是如何实现的情况下,仅凭借想象就可以谈论很多事情,如同写科幻小说一样,我想这也是 SICP 为什么用魔法师作为封面的原因,因为这个职业的核心能力就是使用咒语, 而编程之所以可以成为现代魔法师,是因为这些“咒语”背后有具体的机器把它们变成另外一种物理现实,比如图片,声音,游戏,机器人动作等等。
注:传统“咒语”的语义只可以被人脑直接解释,比如诸葛亮舌站群儒就是因为他说的话直接被其他人脑理解从而影响当时的天下大势,但计算机使得编程语言这种咒语可以直接作用在非人类对象上,从而绕过具体的人而对物理世界产生影响。
自上而下的想象
当要落实这种想象的时候,就需要向下一层去索要功能,比如你显然知道计算机屏幕上是可以绘制图片的,但它们可能是某种底层的远古语言或框架的实现,这距离当前谈论的抽象层很远,因此继续找中间的抽象层去填补间隔,比如我发现 python 的 matplotlib 就可以方便地绘图,而 python 语言也能实现以上所谈论的递归,因此我要做的是先把 painter 以上的抽象层的 scheme 代码翻译到 python,然后找到 matplotlib 的文档,了解如何能够用它的接口实现 painter 对象即可。
也就是说,本文里涉及的真正的“新”的实现,仅仅是用 matplotlib 来支持对 painter 对象的绘制,这是以下抽象层里的最底层部分:
+-----------------------+
| 递归绘制层 | (可以不用递归)
+-----------------------+
^
|
+-------------------------------+
|仿射变换组合层(transform_painter) | (可以用矩阵乘法替代)
+-------------------------------+
^
|
+-----------------------+
| painter 和基础变换层 | (可以用类而不是 lambda 闭包)
+-----------------------+
^
|
+-----------------------+
| 向量和线段层 (vect,segs) | (可以用 numpy array 替代)
+-----------------------+
^
|
+-----------------------+
| 绘制层 (matplotlib) | (可以用其他绘制工具替代)
+-----------------------+
书本里是逐层向下把各个层都实现了, SICP 不断强调通过这种分层抽象来控制软件复杂度,比如书的章节安排也是在自上而下分层的,前两章介绍 scheme 高层的使用方式;第三章走向下一层,开始介绍解释器的原理,即 scheme 是如何对表达式求值的;第四章用 scheme 实现自身的解释器;第五章则是介绍如何在更底层在机器上实现 scheme 。
实际上,在这个分层建筑中向下走,向上爬或者横向游走几乎都是没有尽头的:
- 向上可以写出越来越庞大而复杂的应用软件和机器,以至于一些人机交互接口的熟悉就够你花很多年了, 比如真正精通 execl/ppt,熟练开挖掘机,飞机,宇宙飞船。
- 向下进入操作系统,计算机结构,电子工程,物理,直达神秘大自然的馈赠。 书本人为控制了层的跨度,给它划定到了计算机科学或者计算机程序相关的范围。
- 横向则是每一层的设计模式,数学,算法优化等等。比如要正确实现 painter 的变换层,需要线性代数的知识。如果要实现一个更复杂的物理模拟引擎或者某种加密算法,那单这一层里一个算法就可能需要整个本科或研究生需要的知识。即便只谈功能,单个抽象层也足够复杂(和人机交互层类似),比如 linux 内核, opengl,这使得大部分人只需要待在某一层,了解其相邻层的一些接口使用方式,就足以成为领域专家。
这应该也是 SICP 与这个时代需求不太匹配的原因,在计算机产业化之后,分工使得人们很难有精力从某个抽象层或者某个局部领域里(前端、后端)的几个抽象层里抽身出来。在这种情况下,即便看到了整个技术栈,也不会对实际有太多影响,一个不太恰当但似乎对我有所启发的例子是:即便完全不知道地球是如何产生并飘浮在太空中的,人体的组织是如何构造的,感光细胞是如何编码和传递信号的,大脑中对信息的解释是如何运作的,但人类还是存活到了现在,还是可以稳稳地坐着,阅读这篇文章,并理解点什么。
当然这里有点远了,接下来回到 matplotlib 层,并开始向上实现(翻译):
自下向上的实现
plt.plot 绘图的分解动作
参考 python - How to draw a line with matplotlib? - Stack Overflow
plt.plot 的基本用法是 plt.plot(x, y), 其中 x 是平面上所有点的 x 坐标,y 是所有点的 y 坐标。
例如,在点 (1,3) 和 (2,4) 之间连线:
import matplotlib.pyplot as plt
plt.rcParams["figure.figsize"] = (3,3)
plt.plot([1,2], [3,4]);

默认情况下,相邻的点会按传入顺序用线段自动连接,因此,如果要 plot 出一个更复杂的图形,需要考虑该图形是否能一笔划出,为此需要设计每个点绘制的顺序,以下是一个传入顺序混乱的例子:
x = [0.5, 0.0, 1.0, 0.5, 0.3, 0.7]
y = [1.0, 0.7, 0.3, 0.5, 0.0, 0.0]
plt.plot(x, y);
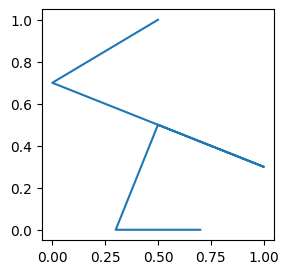
这些点的位置坐标是正确的,但连接的顺序有问题,我们希望点之间是按以下代码里声明的关系相互连接的,但上图则是 按照 head-larm,larm-rarm,rarm-body,body-ltoe,ltoe-rtoe 的连接方式,从而导致了混乱。
head = (0.5, 1)
larm = (0, 0.7)
rarm = (1, 0.3)
body = (0.5, 0.5)
ltoe = (0.3, 0)
rtoe = (0.7, 0)
stick_man = [(head, body), (larm, body), (rarm, body), (ltoe, body),(rtoe, body)]
幸好 plt.plot 还可以传入多组 x 和 y 坐标列表,plot 会自动两两作为一组,因此如果传入 4 个 list,相当于进行“两笔画”,传入 10 个 list 相当于进行 "五笔画", 这种机制能够比较方便地处理不同的点之间的特定连接,比如以下是两笔绘制:
plt.plot([1, 2], [3, 4], [0, 1, 1.4], [1, 2, 3]);
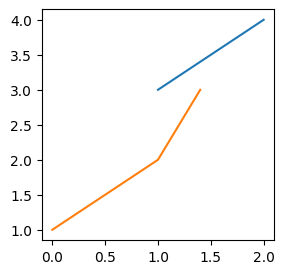
点 (1,3) 与 (2,4) 之间画上了线段(右上),而点 (0, 1), (1, 2), (1.4, 3) 依次构成另外一组连接(左下)
这等价于:
plt.plot([1,2],[3,4])
plt.plot([0, 1, 1.4], [1, 2, 3])
plt.show()
以下函数把 stick_man 里对图形的线段形式描述转成多组 x,y 坐标分离的列表形式,以提供给 plt.plot 做多笔绘制。
def segments2plot(segments):
return sum([list(zip(*seg)) for seg in segments], [])
plt.plot(*segments2plot(stick_man))
plt.show()

接着再引入一个改编自 SICP 2.2.4 Example: A Picture LanguageをPythonでやってみたらデキタ━━━━(゚∀゚)━━━━ッ!! - 牌語備忘録 -pygo 的图片(后文很多函数也基于此文)
meo = [
[[0.0, 0.0], [0.2, 1.0]],
[[0.2, 1.0], [0.3, 0.8]],
[[0.3, 0.8], [0.7, 0.8]],
[[0.7, 0.8], [0.8, 1.0]],
[[0.8, 1.0], [1.0, 0.0]],
[[0.4, 0.6], [0.3, 0.6]],
[[0.3, 0.5], [0.3, 0.6]],
[[0.3, 0.5], [0.4, 0.5]],
[[0.8, 0.6], [0.7, 0.6]],
[[0.7, 0.6], [0.7, 0.5]],
[[0.7, 0.5], [0.8, 0.5]],
[[0.7, 0.4], [0.4, 0.4]]
]
并且提供一个可以绘制多个图形的 render 函数:
def render(*all_segs):
num_plots = len(all_segs)
if num_plots == 0: return
if num_plots == 1:
plt.plot(*all_segs[0])
else:
# Calculate the number of rows and columns for the subplot grid
num_cols = min(num_plots, 4)
num_rows = (num_plots+2) // 4
# Create the figure and subplots
fig, axes = plt.subplots(num_rows, num_cols, figsize=(2.8 * num_cols, 2.4 * num_rows))
# Flatten the axes array for easy indexing
axes = axes.flatten()
for i, segs in enumerate(all_segs):
ax = axes[i]
ax.plot(*segs)
plt.tight_layout()
plt.show()
render(segments2plot(stick_man), segments2plot(meo))

vect(point), segment,draw-line 封装
实际上 matplotlib 的实现就已经结束了。接下来只是按照书本的描述用 python 重新翻译 picture-langage 的实现(所有的接口的命名和书本尽可能保持一致)。
先是对点(向量)的构造函数,选择函数以及加法和点乘接口:
def make_vect(x, y):
return (x, y)
def xcor_vect(v):
return v[0]
def ycor_vect(v):
return v[1]
def add_vect(v1, v2):
return make_vect(xcor_vect(v1) + xcor_vect(v2),
ycor_vect(v1) + ycor_vect(v2))
def sub_vect(v1, v2):
return make_vect(xcor_vect(v1) - xcor_vect(v2),
ycor_vect(v1) - ycor_vect(v2))
def scale_vect(a, v):
return make_vect(a * xcor_vect(v), a * ycor_vect(v))
然后是对线段:
def make_segment(p1, p2):
return (p1, p2)
def start_segment(s):
return s[0]
def end_segment(s):
return s[1]
def draw_line(p1, p2):
return segments2plot([make_segment(p1, p2)])
render(draw_line(make_vect(0,0), make_vect(1,1)))
Frame 的构造
以上 vect 和 segment 可以让我们组合绘制出类似火柴人的对象,但还无法对整个对象进行移动或者翻转等变换,比如为了把火柴人向左边平移,就需要对所有点的 x 减去一个数,而为了放大火柴人,则需要对每个左边点乘以一个数, 这些操作实际都是并行地针对图片里每一个点的,因此它们都可以抽象成一个对象,书本中称为 frame, 它是一个坐标系, 接收的是三个向量:中心点,两个主轴。
def make_frame(origin, edge1, edge2):
return (origin, edge1, edge2)
def origin_frame(frame):
return frame[0]
def edge1_frame(frame):
return frame[1]
def edge2_frame(frame):
return frame[2]
def frame_coord_map(frame):
return lambda v:add_vect(
origin_frame(frame),
add_vect(scale_vect(xcor_vect(v),
edge1_frame(frame)),
scale_vect(ycor_vect(v),
edge2_frame(frame))))
frame_coord_map 接收一个 frame 坐标系,返回一坐标变换函数,该函数接收一个向量,对这个向量进行 frame 所描述的坐标变换后返回新的向量。
如果用线性代数的语言来描述,frame 编码的是一个仿射变换, edge1 和 edge2 是仿射变换中矩阵 A 的两列, origin 是偏置, frame_coord_map(frame)(vect) 是在做仿射变换。例如,假设要对图片里所有的点上下翻转,一种做法是:
- 先对向量围绕 x 轴进行翻转, (x,y) 得到 (x,-y), 对应的线性变换的矩阵 A 的两个列就是 (1,0) 和 (0,-1), 这样 x(1,0)+y(0,-1) 才等于 (x,-y).
- 但这样做图形就跑出画布了(本文中所有图片都绘制在 0<=x<=1 和 0<=y<=1 的单位正方形中),为了把它移回画布,要对所有点加上偏置 b=(0,1)
- 因此这个 frame 的构造是 make_frame((0, 1), (1, 0), (0, -1)) ,而 frame_coord_map(frame)(x) 等价于对每个点 x 做仿射变换 Ax+b
可以把 frame 展示出来:
def plot_frame(frame):
o = origin_frame(frame)
v1 = add_vect(o, edge1_frame(frame))
v2 = add_vect(o, edge2_frame(frame))
return segments2plot((((0, 0), o), (o, v1), (o, v2)))
标准坐标系:
standard_frame = make_frame(make_vect(0, 0),
make_vect(1, 0),
make_vect(0, 1))
把原点移动到 (0.5,0.5) 位置,并且把 x 轴向上倾斜 45 度的坐标系:
dia_frame = make_frame(make_vect(0.5,0.5), make_vect(1,1), make_vect(0,1))
render(plot_frame(standard_frame), plot_frame(dia_frame))
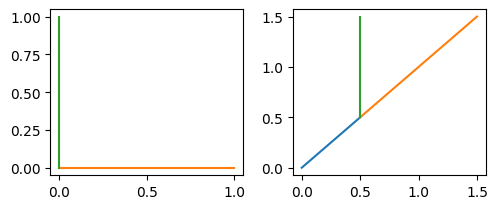
把标准坐标系里的点 (1,1) 传给 dia_frame 的变换函数后,得到的坐标是 (1.5, 2.5)
print(frame_coord_map(dia_frame)(make_vect(1,1)))
(1.5, 2.5)
Painter 构造
painter 是一个函数闭包,构造它时,它传入原始点(标准坐标系的坐标),因此闭包里就保存了这些数据, 而返回的函数等待接收 frame 对象(也就是对这些点的视角),当传入一个特定的 frame ,原始转换会经过转换返回新的坐标系中得到最终坐标,然后调用 draw_line 进行绘制:
由于只从 segment 进行构造,因此其构造函数名称就称为 segment_list:
def segments2painter(segment_list):
return lambda frame: sum([draw_line(
frame_coord_map(frame)(start_segment(segment)),
frame_coord_map(frame)(end_segment(segment)))
for segment in segment_list],[])
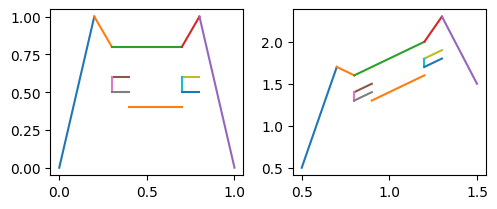
以下是将原点移动到 (0.5,0.5) 并对 x 轴向上倾斜 45 度的 frame 作用于在图片上的效果
meo_painter = segments2painter(meo)
render(meo_painter(standard_frame), meo_painter(dia_frame))
transform painter 的各类基础操作抽象层
def transform_painter(painter, origin, corner1, corner2):
return lambda frame:painter(make_frame(
frame_coord_map(frame)(origin),
sub_vect(frame_coord_map(frame)(corner1),
frame_coord_map(frame)(origin)),
sub_vect(frame_coord_map(frame)(corner2),
frame_coord_map(frame)(origin))))
个人觉得以上函数是 picture language 实现层里最难理解的实现,它需要读者对 scheme 闭包的语法以及坐标转换的语义都有清晰的理解,放到更大背景下,它是在用函数式编程实现仿射变换的组合(composition)。
先看看上层函数是怎么使用 transform_painter 的,比如以下是对图片旋转 90 度的操作:
def rotate90(painter):
return transform_painter(painter,
make_vect(1.0, 0.0),
make_vect(1.0, 1.0),
make_vect(0.0, 0.0))
前面说到,对于 rotate90, beside 等变换函数,属于 picture langage 的内置基本操作,能够接受一个 painter 对象,再返回另一个 painter 对象,这种封闭性质和 scheme 的变成范式不谋而合(当然是为了 scheme 而专门设计的),因此可以编写出更多高层的递归变换模式。
从以上 rotate90 是实现来看,它是对 transform_painter 这个通用转换一种特化形式,也就是给 transform_painter 的后三个参数一个预定义的值之后得到的新的 transform_painter,在 python 中有实现这类函数特化模式的语法: functools.partial
from functools import partial
def adds(a,b,c):
return a+b+c
add3 = partial(adds, b=1,c=2)
add3(3)
6
那么 rotate90 可以写成:
rotate90 = partial(transform_painter,
origin=make_vect(1.0, 0.0),
corner1=make_vect(1.0, 1.0),
corner2=make_vect(0.0, 0.0))
这里想表明的是,对图片的所有基础操作,如 rotate90, beside 实际都等价于带有预定参数的 transform_painter ,因此图片的转换实际就是:
new_painter=transform_painter(painter, ...)
这里 … 的不同会导致不同的转换,但总体来说,转换就是输入一个 painter 同时返回也是 painter 。
接着再看该函数的签名:
def transform_painter(painter, origin, corner1, corner2):
return lambda frame:painter(make_frame(..frame..))
painter 是一个 lambda 函数:
lambda frame:painter(make_frame(..rotate..frame..))
make_frame 里会使用 origin, corner1, corner2 对 frame 进行变换,我们直接用其语义比如 rotate 来标记。
如果继续调用以上 lambda 函数,给它传入了标准坐标系 standard,那么转换前的 painter 会被调用,但传给它的参数不再是标准坐标系,而是执行 make_frame(..rotate..frame..) 后经过处理的坐标系, 如果 painter 本身是对另一个 old_painter 转换(比如平移)的结果,那它就是:
painter = lambda frame1:old_painter(make_frame(..shift..frame1..))
用以上等式右侧的 lambda 去替换
lambda frame:painter(make_frame(..rotate..frame..))
中的 painter 就得到:
lambda frame:(lambda frame1:old_painter(make_frame(..shift..frame1..)))(make_frame(..rotate..frame..))
传入标准坐标系 standard 后最终执行的是:
old_painter(make_frame(..shift..(make_frame(..rotate..standard..))..))
也就是说,如果对同一个 painter 先进行 shift 转换再进行 rotate,那么在最后执行的时候是先对 frame 进行 rotate 再 shift 。
举个例子,矩阵 A,B,C, 分别对应了三个二维空间的线性变换,可以先用矩阵乘法计算 AB, 然后将其结果和 C 相乘得到 ABC, 变换的组合顺序是先 A 后 B 再 C ,但当把 ABC 应用到平面上具体的点 x 上时,计算 ABCx 结果是先对 x 应用 C 变换,然后 B, 最后 A 。(仿射变换顺序也是一样的)
最后看 transform_painter 是如何构造新的 frame 的:
return lambda frame:painter(make_frame(
frame_coord_map(frame)(origin),
sub_vect(frame_coord_map(frame)(corner1),
frame_coord_map(frame)(origin)),
sub_vect(frame_coord_map(frame)(corner2),
frame_coord_map(frame)(origin))))
注意 frame_coord_map 函数不是对线性变换进行组合的(比如不是进行矩阵乘法 AB),而是对单个向量进行仿射变换的,但由于作者约定传入 transform_painter 的 origin, corner1, corner2 是 1x1 的正方形里向量点的绝对位置,这个设计很是巧妙,
- 一方面使得可以直接复用这个函数来进行变换的组合,从而避免矩阵乘法,使得代码变得优雅,但因为 make_frame 接受的是,
- 另一方面使得接下来构建各种特定的转换变得更直观,比如要把图片上下翻转,那么实际就是是把图片的左下角和右上角对调, 于是原点坐标从 (0,0) 移动到 (0,1), 整个 x 轴移动到了 x=1 的位置,因此原本的 x 轴上的单位向量的端点变成了 (1,0), 原本 y 轴上的单位向量的端点就变成了 (0,0) 。
如果是用标准仿射变换的写法,那么偏移项是 (0,1), x 方向不变,因此 (1,0), y 方向翻转了,因此是 (0,-1), 具体见下一小节。
通过 transform_painter 包装出的不同的转换(只是取一个更直观的名字):
def flip_vert(painter):
return transform_painter(painter,
make_vect(0.0, 1.0),
make_vect(1.0, 1.0),
make_vect(0.0, 0.0))
def shrink_to_upper_right(painter):
return transform_painter(painter,
make_vect(0.5, 0.5),
make_vect(1.0, 0.5),
make_vect(0.5, 1.0))
def rotate90(painter):
return transform_painter(painter,
make_vect(1.0, 0.0),
make_vect(1.0, 1.0),
make_vect(0.0, 0.0))
def squash_inwards(painter):
return transform_painter(painter,
make_vect(0.0, 0.0),
make_vect(0.65, 0.35),
make_vect(0.35, 0.65))
def beside(painter1, painter2):
split_point = make_vect(0.5, 0.0)
paint_left = transform_painter(painter1,
make_vect(0.0, 0.0),
split_point,
make_vect(0.0, 1.0))
paint_right = transform_painter(painter2,
split_point,
make_vect(1.0, 0.0),
make_vect(0.5, 1.0))
return lambda frame:sum([paint_left(frame), paint_right(frame)],[])
def flip_horiz(painter):
return transform_painter(painter,
make_vect(1.0, 0.0),
make_vect(0.0, 0.0),
make_vect(1.0, 1.0))
def rotate180(painter):
return rotate90(rotate90(painter))
def rotate270(painter):
return transform_painter(painter,
make_vect(0.0, 1.0),
make_vect(0.0, 0.0),
make_vect(1.0, 1.0))
def below(painter1, painter2):
return rotate90(beside(rotate270(painter1), rotate270(painter2)))
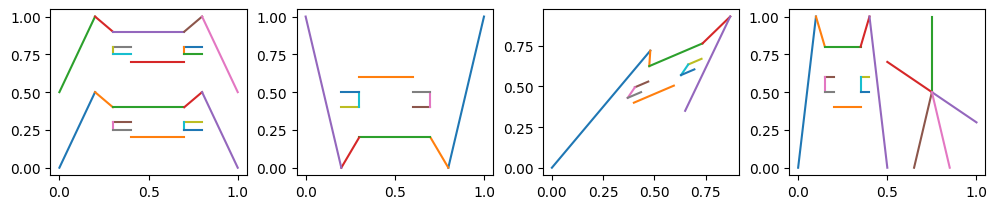
转换后传入标准坐标系即可以“渲染”:
stick_man_painter = segments2painter(stick_man)
render(below(meo_painter, meo_painter)(standard_frame),
rotate180(meo_painter)(standard_frame),
squash_inwards(meo_painter)(standard_frame),
beside(meo_painter, stick_man_painter)(standard_frame))
矩阵组合的写法
可以用标准矩阵乘法来实现 transform_painter 里 frame 的组合:
import numpy as np
def frame_compose(frame1, frame2):
x1, x2 = edge1_frame(frame1)
y1, y2 = edge2_frame(frame1)
p1, p2 = edge1_frame(frame2)
q1, q2 = edge2_frame(frame2)
# matrix multiplication
arr1 = np.array([[x1, y1], [x2, y2]])
arr2 = np.array([[p1, q1], [p2, q2]])
new_arr = arr1 @ arr2 # 如果写成 arr2 @ arr1 就会出错
e11, e12 = new_arr[0]
e21, e22 = new_arr[1]
new_frame = make_frame(
frame_coord_map(frame1)(origin_frame(frame2)),
make_vect(e11, e21),
make_vect(e12, e22)
)
return new_frame
def transform_painter(painter, origin, corner1, corner2):
def _painter(frame):
old_frame = make_frame(origin, corner1, corner2)
new_frame = frame_compose(frame, old_frame)
# print("new:", new_frame)
return painter(new_frame)
return _painter
def flip_vert(painter):
# print("flip_vert")
return transform_painter(
painter, make_vect(0.0, 1.0), make_vect(1.0, 0.0), make_vect(0.0, -1.0)
)
def shrink_to_upper_right(painter):
return transform_painter(
painter, make_vect(0.5, 0.5), make_vect(0.5, 0.0), make_vect(0.0, 0.5)
)
def rotate90(painter):
# print("rotate90")
return transform_painter(
painter, make_vect(1.0, 0.0), make_vect(0.0, 1.0), make_vect(-1.0, 0.0)
)
def rotate180(painter):
return rotate90(rotate90(painter))
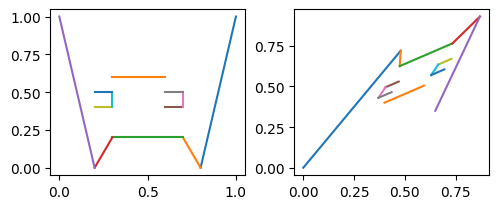
render(rotate180(meo_painter)(standard_frame),
squash_inwards(meo_painter)(standard_frame))
更高层的操作
封装出书本里那些递归模式:
def up_split(painter, n):
if n == 0:
return painter
smaller = up_split(painter, n - 1)
return below(painter, beside(smaller, smaller))
def right_split(painter, n):
if n == 0:
return painter
smaller = right_split(painter, n - 1)
return beside(painter, below(smaller, smaller))
def corner_split(painter, n):
if n == 0:
return painter
up = up_split(painter, n - 1)
right = right_split(painter, n -1)
top_left = beside(up, up)
bottom_right = below(right, right)
corner = corner_split(painter, n - 1)
return beside(below(painter, top_left),
below(bottom_right, corner))
def square_limit(painter, n):
quarter = corner_split(painter, n)
half = beside(flip_horiz(quarter), quarter)
return below(flip_vert(half), half)
render(up_split(meo_painter, 3)(standard_frame),
square_limit(meo_painter, 3)(standard_frame),
square_limit(stick_man_painter, 4)(print_frame))

Sierpinski's triangle
还可以用这个语言来绘制其他的递归性质图像,比如经典的 Sierpinski 三角形。
def triple(painter):
up0 = make_vect(0.25, 0.5)
up1 = make_vect(0.75, 0.5)
up2 = make_vect(0.25, 1)
left0 = make_vect(0, 0)
left1 = make_vect(0.5, 0)
left2 = make_vect(0, 0.5)
right0 = left1
right1 = make_vect(1, 0)
right2 = make_vect(0.5, 0.5)
paint_up = transform_painter(painter, up0, up1, up2)
paint_left = transform_painter(painter, left0, left1, left2)
paint_right = transform_painter(painter, right0, right1, right2)
return lambda frame:sum([paint_up(frame), paint_left(frame), paint_right(frame)], [])
其 base 就是一个三角形,然后缩小三分之一,并且拷贝三份分别放到三个角上 定义一个类似 right_split 或者 up_split 的 triple_split 操作,以及类似 beside 的 triple 操作
def triple_split(painter, n):
if n == 0:
return painter
new = triple_split(painter, n - 1)
return triple(new)
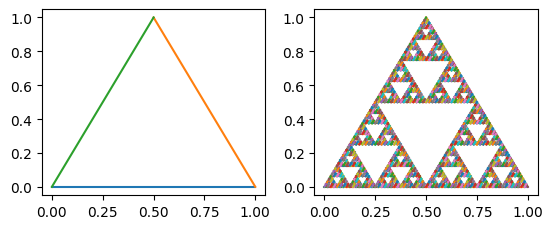
tri_painter = segments2painter([[[0,0], [1,0]], [[1,0],[0.5,1]], [[0,0],[0.5,1]]])
render(tri_painter(standard_frame), triple_split(tri_painter, 6)(standard_frame))
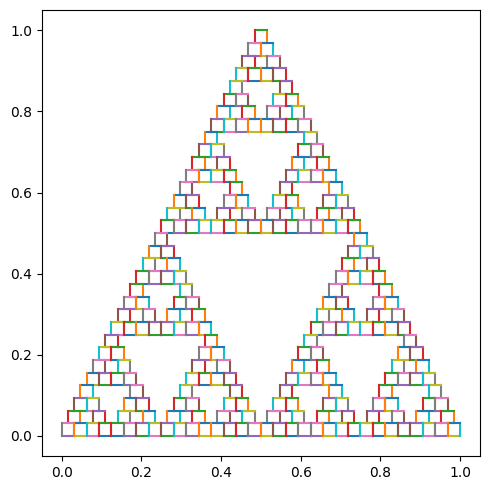
也可以把最初的形状设置为方形
square_painter = segments2painter([[[0,0], [1,0]], [[1,0],[1,1]],
[[1,1],[0,1]], [[0,1],[0,0]]])
render(triple_split(square_painter, 5)(standard_frame))
其他递归图形
picture language 是人为从图片整体上识别或设计出了递归模式,以此实现的程序也按这种递归方式绘制出递归图。
但也可以在识别出图的全局递归模式后,找出局部点的关系,用迭代方式去绘制递归图,这是一种称为 Iterated Function Systems (IFS) 的画法,用它来绘制 Sierpinski triange 的算法描述是:
- 给定初始三角形的三个顶点作为候选点集合
- 从中随机选一个点作为 start
- 将初始点投影在图上(也可以最后一起投影),从候选点中随机取一个点作为 end,求出 start 和 end 的中点,把中点作为新的 start,投影在图上,如此迭代
以此得到的图是:
import random
def ifs_generator(sets = [(0, 0), (1, 0), (0.5, 0.5)]):
start = (0, 0)
while 1:
target = random.choice(sets)
start = ((start[0] + target[0])/2, (start[1] + target[1])/2)
yield start
def ifs_draw(generator, n=10000):
dots = []
for _ in range(n):
dots.append(next(generator))
plt.plot(*zip(*dots), ".")
plt.show()
ifs_draw(ifs_generator())

这种方式为什么可行?
- 先从图片整体上看,假设我们已经得到了最终递归的图,那么可以把它每条边缩小一倍后再分别放到三个角上, 又得到了原始的图。也就是说,先缩放再平移到任意一个角会保持图形不变(这也叫作分形,即局部和整体结构上是一样的)。
- 更细地看,要从最大三角形得到左下角的和它一样的边长减半的三角形,要做的只是把大三角形上所有点的坐标除以 2 , 也就是从大三角形里随机选一个点作为 start, 然后选 (0,0) 作为 end 求平均得到的点。
- 同理,要从最大三角形得到上方和它一样的三角形,要做的是从大三角形里随机选一个点作为 start, 将顶部的点 (0.5,0,5) 作为 end 二者求平均。(将原始图里的点和任意一个顶点求平均就相当于缩放然后再朝着顶点方向平移)
- target = random.choice(sets) 就是每次从大三角形里随机选出一个顶点,而 start 是求平均后得到的新点,它一定是在最终的大三角形里,每次迭代就是个这个点朝着三个方向中之一做一次缩放并平移。
另外,这种实现完全避开了对 picture-langage 的构造,你不需要为了画出分形(递归图)而去发明(或扩展)一种支持高阶递归的语言, 如果某个计算机汇编指令里有 plot(x,y) 命令(或者自己根据生成的坐标点手绘),那么你完全可以用汇编甚至图灵机级别的指令来写出这个程序, SICP 里谈论的大部分关于“程序构造”的知识,那座巨大的按抽象级别分层的建筑,你都可以无视, 因为这种机制更接近大自然的演化而非人为设计。
既然演化就可以出现这种看似精心设计的分形,那么自然会有一些图形的出现并不依托于人为事先勾勒出的蓝图,比如参考 Fractals with Python. Visualizing the beautiful: Mandelbrot… | by Dhananjay Budaraju | Analytics Vidhya | Medium, 可以画出:
from numpy import newaxis
def compute_mandelbrot(N_max, some_threshold, nx, ny):
# A grid of c-values
x = np.linspace(-2, 1, nx)
y = np.linspace(-1.5, 1.5, ny)
c = x[:,newaxis] + 1j*y[newaxis,:]
# Mandelbrot iteration
z = c
for j in range(N_max):
z = z**2 + c
mandelbrot_set = (abs(z) < some_threshold)
return mandelbrot_set
mandelbrot_set = compute_mandelbrot(50, 50., 601, 401)
plt.imshow(mandelbrot_set.T, extent=[-2, 1, -1.5, 1.5])
plt.show()

在代码形式上,它和前一个例子是类似的,是一种迭代生成点的过程,但和前一个例子不同的是,它在局部代码上的解释变得非常困难,前一个例子还可以用仿射变换来统一描述,但该图形之所以形成递归,并不是一条规则就能说清的,需要用混沌、非线性系统相关的语言来描述(也可以说这种规律编码在了复数运算的数值规律里,但这就像说神经网络学到的规则都在参数里一样,并没有提供额外的解释信息)。这种情况下,你不是可选择性地忽视抽象层大厦,反而是这座分层的现代工业化结构在它面前自动变得迂腐且无所适从,比如你可以尝试先构思出这种分形,然后修改 picture-langage ,用组合递归的方式把它绘制出来?
更多类型的绘制分形图方法,可以参考:
A simple introduction to the world of fractals using python | by godha lakshmi | Medium